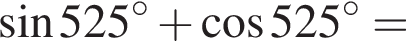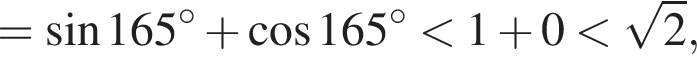Решите систему неравенств: 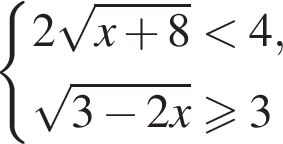 и укажите количество целых решений системы неравенств.
и укажите количество целых решений системы неравенств.
1) 2
2) 1
3) 5
4) 3
5) 4
Решение. Второе неравенство после возведения в квадрат дает
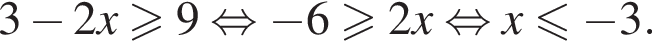
Первое неравенство определено при 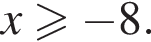 При таких значениях x поделим неравенство на 2 и возведем в квадрат. Получим
При таких значениях x поделим неравенство на 2 и возведем в квадрат. Получим
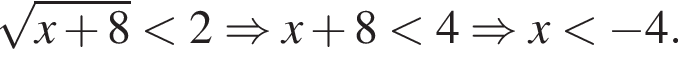
Совмещая все условия, получаем 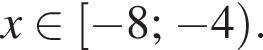 На этом промежутке 4 целых числа: −8; −7; −6; −5.
На этом промежутке 4 целых числа: −8; −7; −6; −5.
Правильный ответ указан под номером 5.
Ответ: 5
23
5

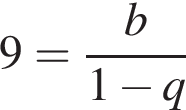 и
и 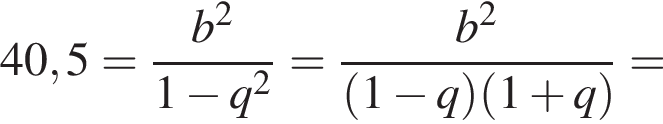

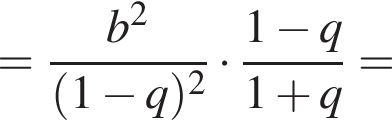
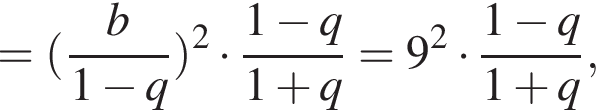
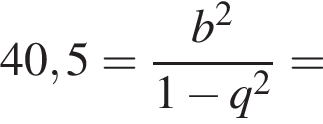
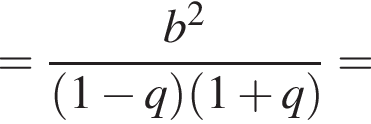
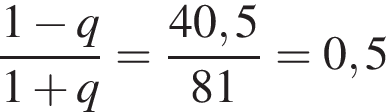

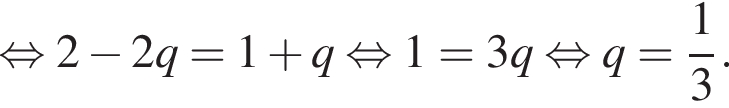

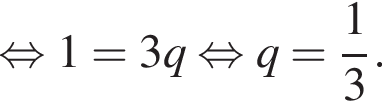
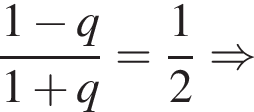
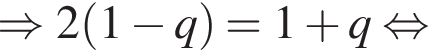
 раза меньше предыдущего. Вычислим их и посчитаем сумму.
раза меньше предыдущего. Вычислим их и посчитаем сумму. 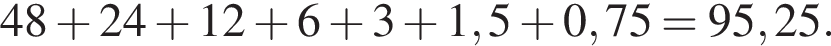
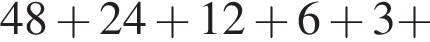


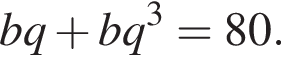 Значит,
Значит, 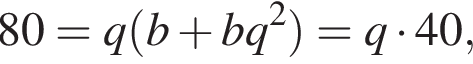
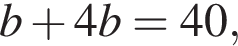 откуда
откуда 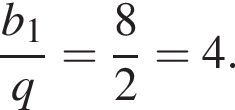
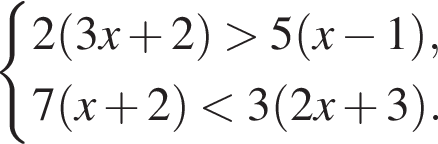
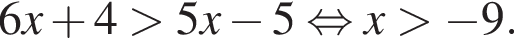

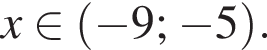 Целых чисел среди них три: −8; −7; −6.
Целых чисел среди них три: −8; −7; −6.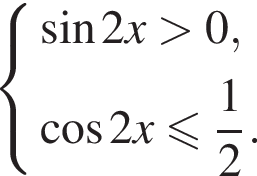
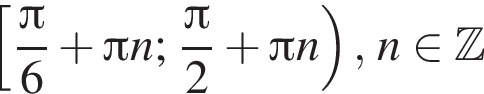
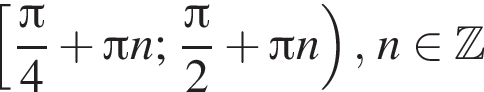
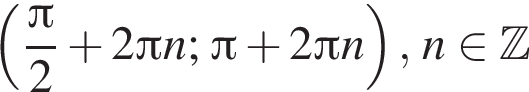
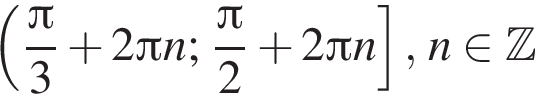
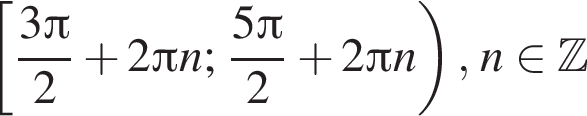
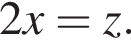 На единичной окружности (см. рисунок) отметим дуги, на которых
На единичной окружности (см. рисунок) отметим дуги, на которых 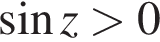 и
и 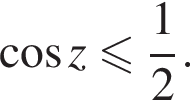 Пересечением этих дуг будет дуга
Пересечением этих дуг будет дуга 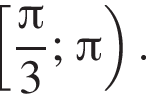 Значит,
Значит, 
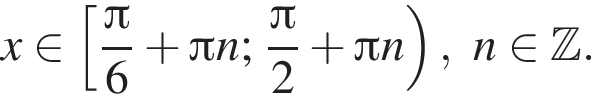
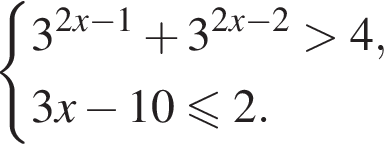
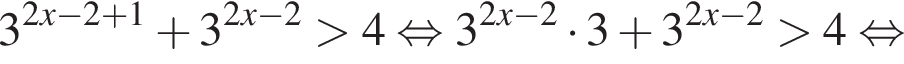
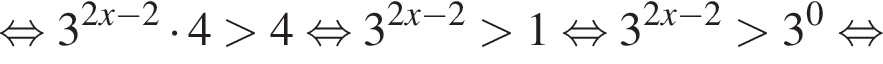

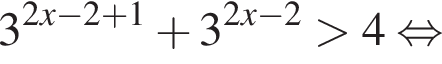
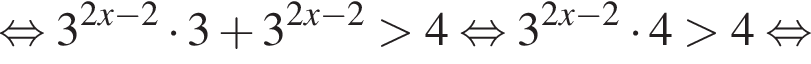

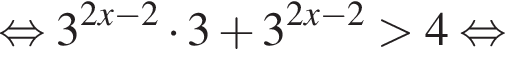
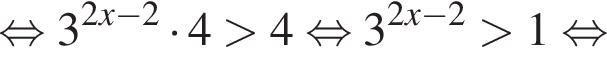


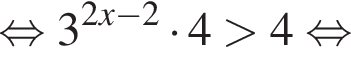
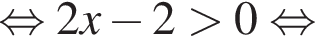
 откуда
откуда 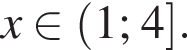
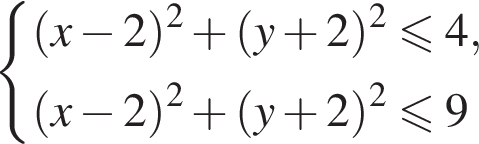
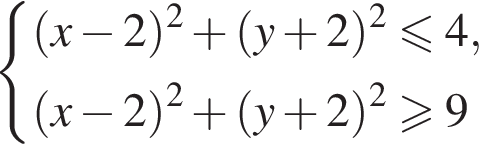
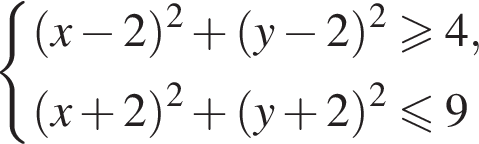
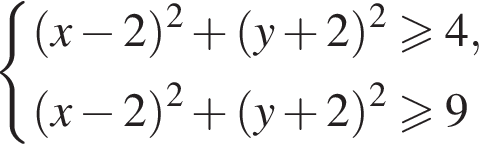
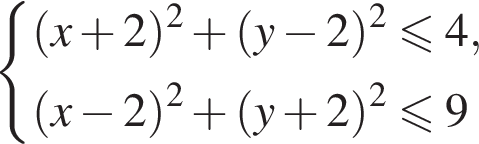
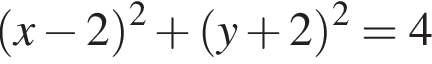 и
и 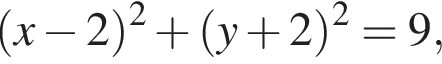 поэтому ответом будет первая система.
поэтому ответом будет первая система.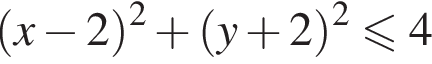 есть еще только во второй системе, но ее второе неравенство задает внешнюю часть круга, поэтому у системы вообще нет решений.
есть еще только во второй системе, но ее второе неравенство задает внешнюю часть круга, поэтому у системы вообще нет решений. где (x; y) — решение системы уравнений
где (x; y) — решение системы уравнений  причем y < 0.
причем y < 0.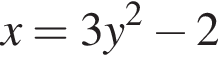 и подставить это выражение в первое уравнение. Получим
и подставить это выражение в первое уравнение. Получим 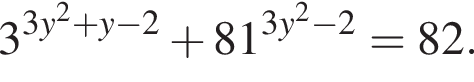
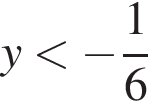 оба показателя степени убывают, поэтому оба слагаемых и их сумма убывают. Значит, на промежутке
оба показателя степени убывают, поэтому оба слагаемых и их сумма убывают. Значит, на промежутке 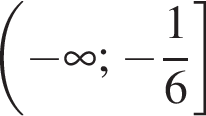 может быть не более одного корня. Подбором находим, что
может быть не более одного корня. Подбором находим, что 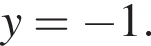 Тогда
Тогда 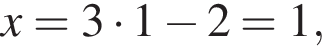 а искомая сумма
а искомая сумма 
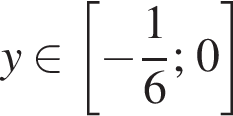 оба показателя степени отрицательны, поэтому сумма двух слагаемых не превосходит
оба показателя степени отрицательны, поэтому сумма двух слагаемых не превосходит 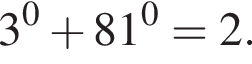 На этом промежутке нет корней. Положительные значения y исследовать не нужно, так как по условию y < 0.
На этом промежутке нет корней. Положительные значения y исследовать не нужно, так как по условию y < 0.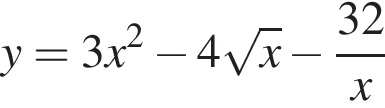 в точке
в точке 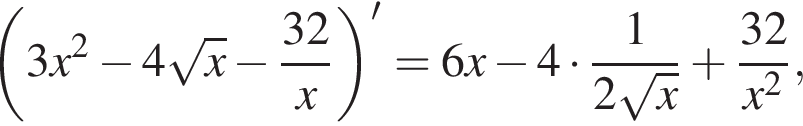
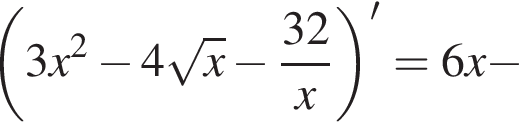
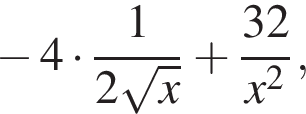
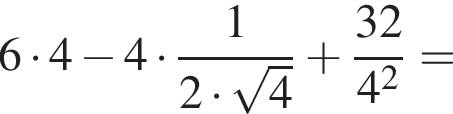
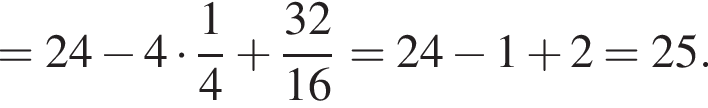
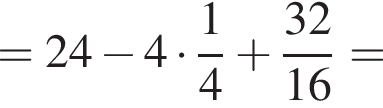
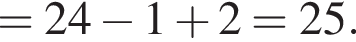
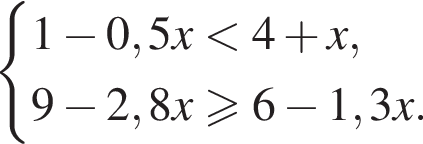
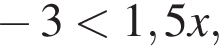 то есть
то есть 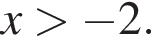 Преобразуя второе неравенство, получим
Преобразуя второе неравенство, получим 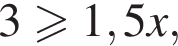 откуда
откуда 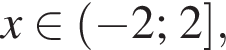 а целыми положительными решениями
а целыми положительными решениями 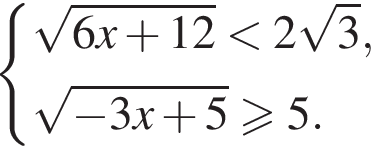
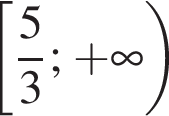
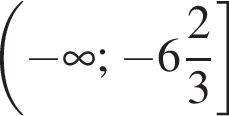
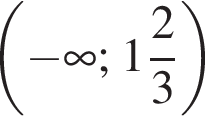
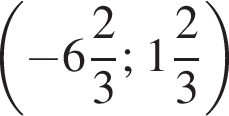
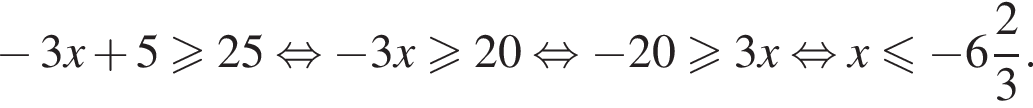

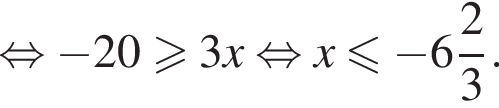
 отрицательно и первое неравенство неопределённо. Значит, у системы нет решений.
отрицательно и первое неравенство неопределённо. Значит, у системы нет решений.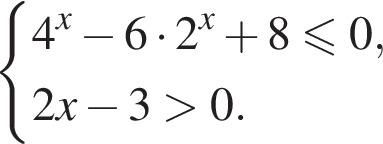
 Преобразуем первое неравенство
Преобразуем первое неравенство
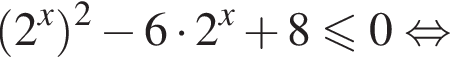

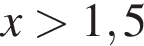 первый множитель положителен, значит, неравенство сводится к
первый множитель положителен, значит, неравенство сводится к 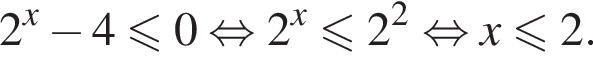


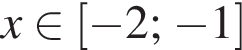
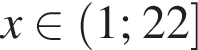
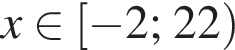
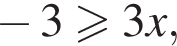 то есть
то есть  При таких x первое неравенство выполнено автоматически, если только подкоренное выражение неотрицательно, что бывает при
При таких x первое неравенство выполнено автоматически, если только подкоренное выражение неотрицательно, что бывает при 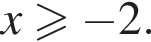 Итак, ответ
Итак, ответ 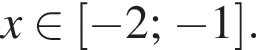
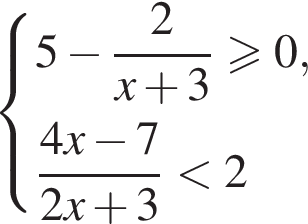
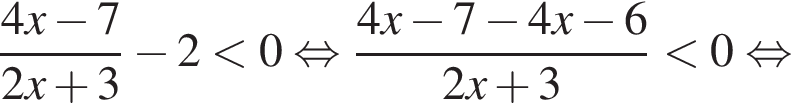
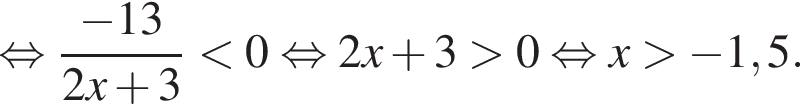
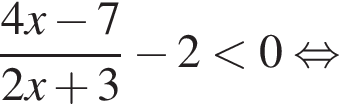
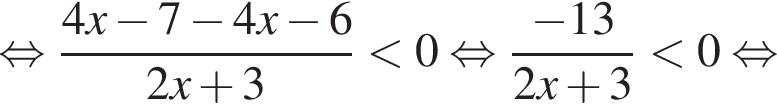
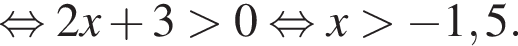
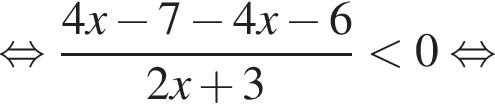
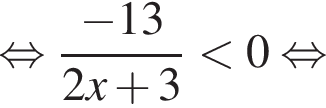
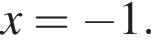 Поскольку оно подходит и в первое неравенство, оно-то и будет ответом.
Поскольку оно подходит и в первое неравенство, оно-то и будет ответом.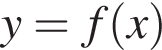 в точке
в точке 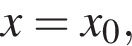 если
если 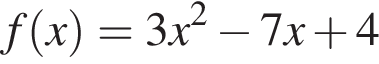 и
и 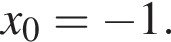
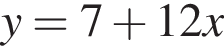
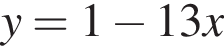
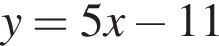
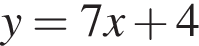
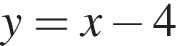
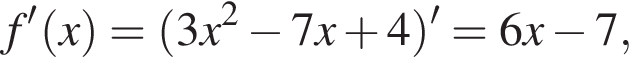 то
то 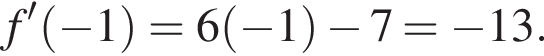 Кроме того,
Кроме того, 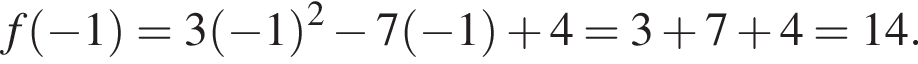
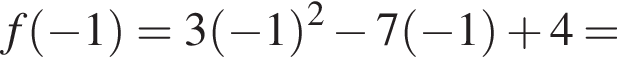


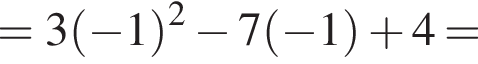
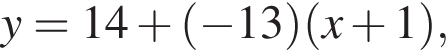 то есть
то есть 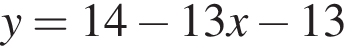 или
или 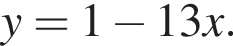
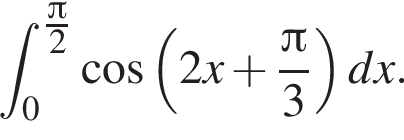
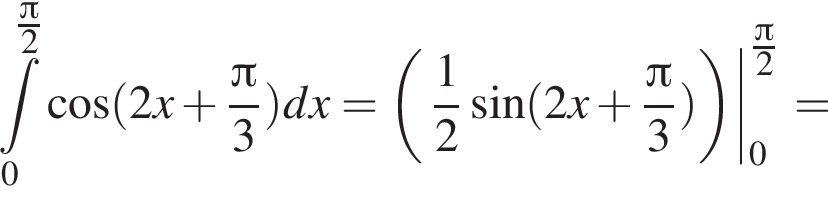
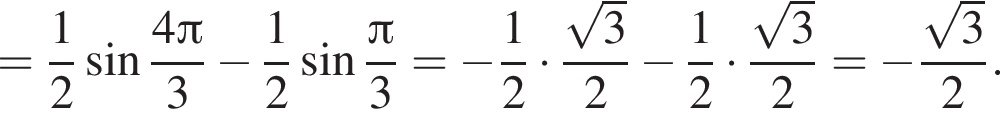
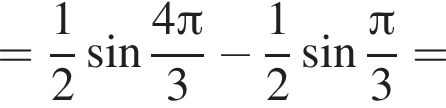
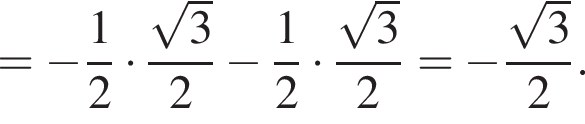
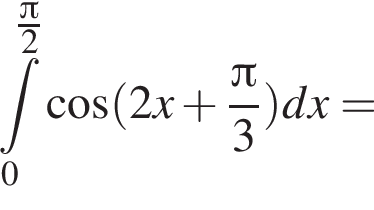
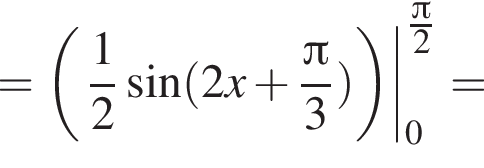
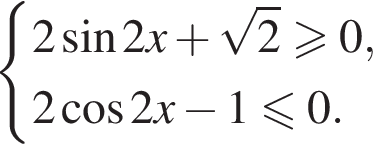
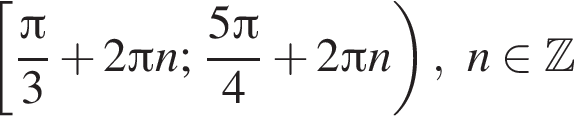
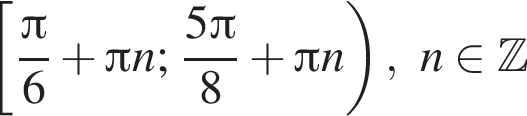
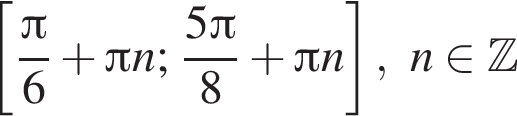
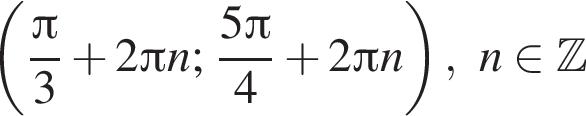
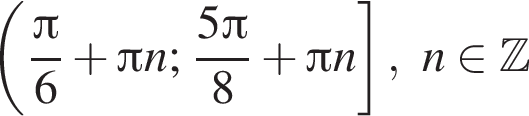
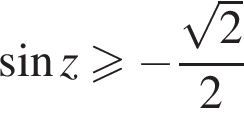 и
и 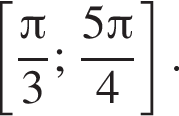 Значит,
Значит, 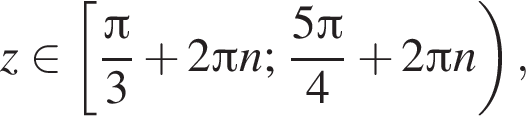
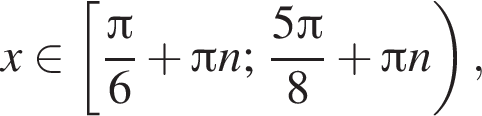
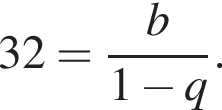
 при этом они тоже образуют бесконечно убывающую геометрическую прогрессию. Значит,
при этом они тоже образуют бесконечно убывающую геометрическую прогрессию. Значит, 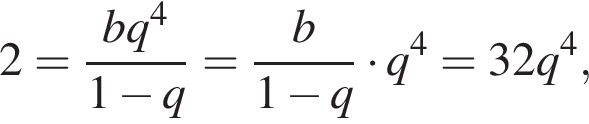
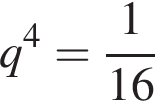 и
и 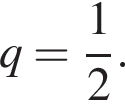 Тогда
Тогда 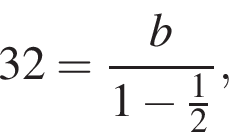 поэтому
поэтому  или
или 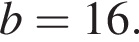
 а
а 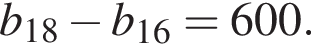
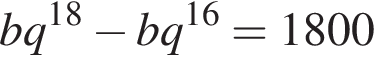 и
и  Значит,
Значит, 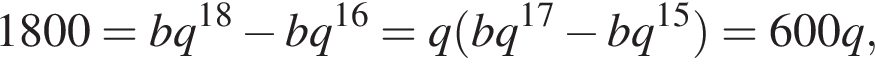
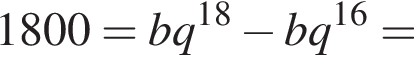
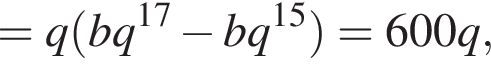
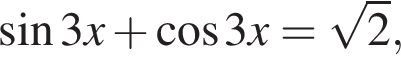 который принадлежит числовому интервалу (90°; 180°).
который принадлежит числовому интервалу (90°; 180°).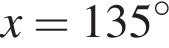 получаем
получаем 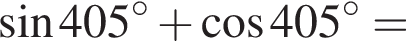

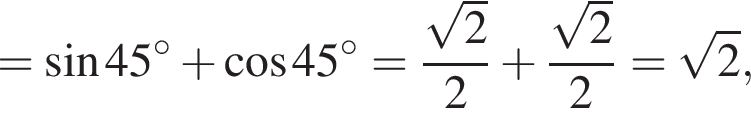

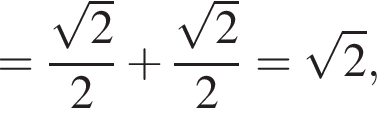
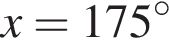 получаем
получаем