Упростите выражение: 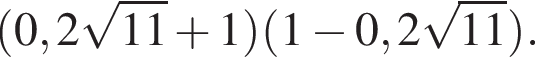
1) 0,56
2) 0,78
3) −0,56
4) −0,78
5) 0,44
Решение. Преобразуем исходное выражение:
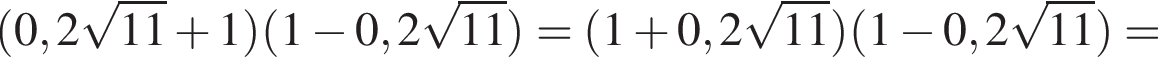
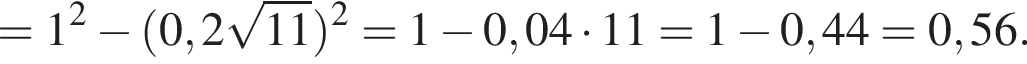
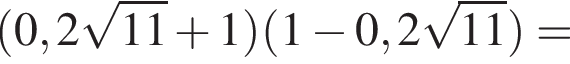
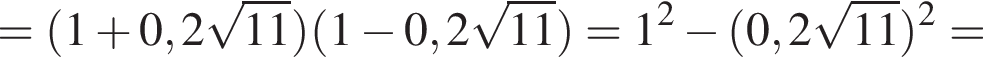

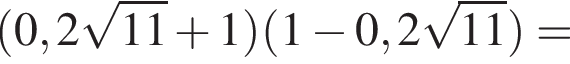
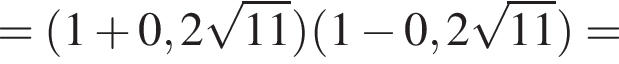
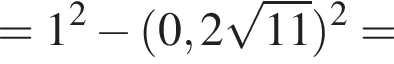

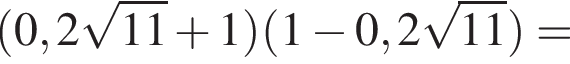
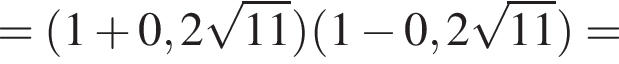
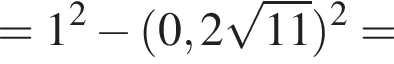
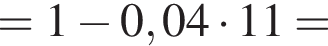
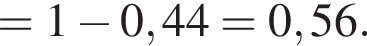
Правильный ответ указан под номером 1.
Ответ: 1
11
1
Упростите выражение: 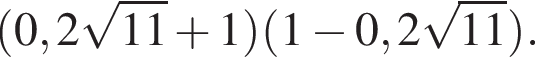
Решить уравнение: 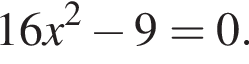
Решите систему уравнений: 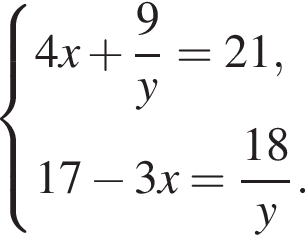
Токарь, делая по 54 детали в час, изготовил все детали за 5 часов. За сколько часов токарь изготовит все детали, если будет делать по 15 деталей в час?
Найдите область определения функции 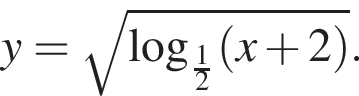
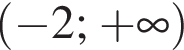
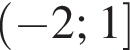
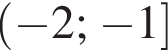
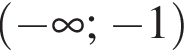
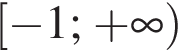
Решите систему уравнений: 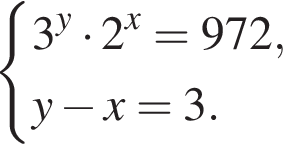
В арифметической прогрессии найдите a7, если 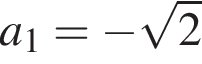 и
и 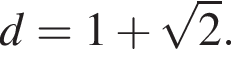
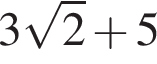
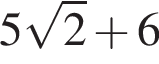
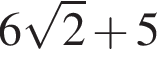
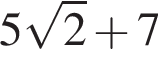
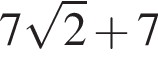
Найдите область значений квадратичной функции: 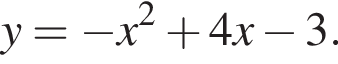
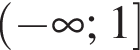
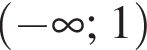
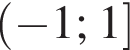

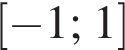
Из круга радиусом 10 вырезали квадрат наибольшего размера. Площадь оставшейся части круга при 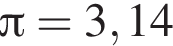 равна
равна
Найдите объем правильной четырехугольной усеченной пирамиды, если стороны ее основания 1 см и 9 см, а высота 6 см.
Числовая последовательность задана условиями 
 Какое из указанных чисел равно x3?
Какое из указанных чисел равно x3?
Значение переменной х, при котором верно неравенство: 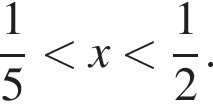
Решите систему неравенств: 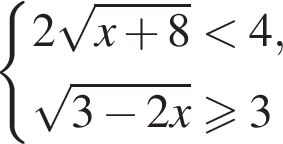 и укажите количество целых решений системы неравенств.
и укажите количество целых решений системы неравенств.
Найдите площадь заштрихованной фигуры:
К окружности проведена секущая CA. Треугольник BOE равносторонний, CA = 12. Длина касательной CE равна
Значение частного
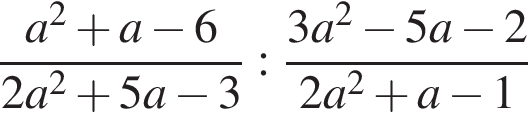
равно
На рисунке радиусы касающихся окружностей с центрами O1 и O2 равны 7 и 3. К окружностям проведена общая касательная BC. Расстояние между точками касания равно:
На заводе работают токари и слесари, число которых относится соответственно как 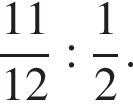 Сколько всего рабочих на заводе, если токарей на 95 больше, чем слесарей?
Сколько всего рабочих на заводе, если токарей на 95 больше, чем слесарей?
Решите систему неравенств: 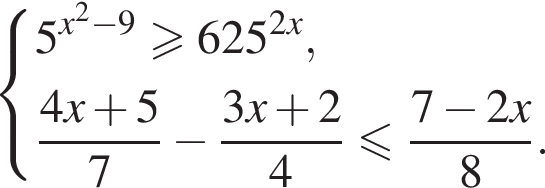
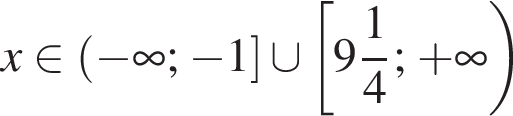
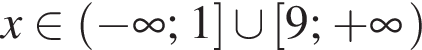
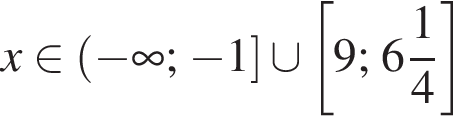
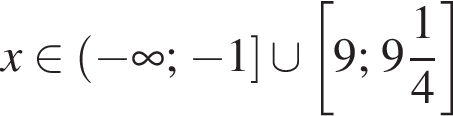
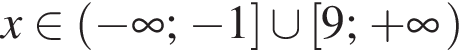
Двугранный угол равен 60°. Из точки N на его ребре в гранях проведены перпендикулярные ребру отрезки NB = 8 см, AN = 2 см. Найдите длину AB.
Строительной компании дали задание построить детскую игровую площадку, в которой должен быть домик в виде башни. Коническая крыша башни имеет диаметр 6 м и высоту 2 м. Для этого купили листы кровельного железа размерами 0,7 м × 1,4 м. На швы и обрезки тратится 10 % от площади крыши.
Чему равна площадь одного кровельного листа?
Строительной компании дали задание построить детскую игровую площадку, в которой должен быть домик в виде башни. Коническая крыша башни имеет диаметр 6 м и высоту 2 м. Для этого купили листы кровельного железа размерами 0,7 м × 1,4 м. На швы и обрезки тратится 10 % от площади крыши.
Чему равна площадь поверхности башни?
 м2
м2 м2
м2 м2
м2 м2
м2Строительной компании дали задание построить детскую игровую площадку, в которой должен быть домик в виде башни. Коническая крыша башни имеет диаметр 6 м и высоту 2 м. Для этого купили листы кровельного железа размерами 0,7 м × 1,4 м. На швы и обрезки тратится 10 % от площади крыши.
Сколько нужно использовать материала (кровельного железа) для покрытия крыши с учетом швов и обрезок? (округлите до целых). 
Строительной компании дали задание построить детскую игровую площадку, в которой должен быть домик в виде башни. Коническая крыша башни имеет диаметр 6 м и высоту 2 м. Для этого купили листы кровельного железа размерами 0,7 м × 1,4 м. На швы и обрезки тратится 10 % от площади крыши.
Какое количество листов понадобится для башни?
Строительной компании дали задание построить детскую игровую площадку, в которой должен быть домик в виде башни. Коническая крыша башни имеет диаметр 6 м и высоту 2 м. Для этого купили листы кровельного железа размерами 0,7 м × 1,4 м. На швы и обрезки тратится 10 % от площади крыши.
Во сколько раз увеличится объем конуса, если его радиус увеличить в 4 раза, а высоту оставить прежней?
Найдите значение выражения 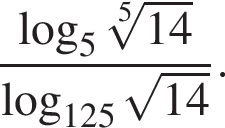
Корнями уравнения 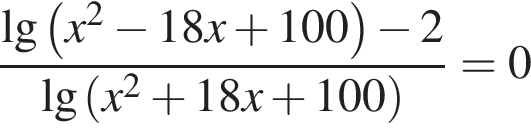 являются?
являются?
Какому промежутку принадлежит сумма (x + y), где (x; y) — решение системы уравнений: 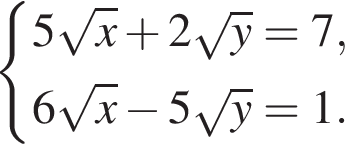
Двое рабочих изготовили 60 деталей за время t. Производительность первого составляет ![]() производительности второго. Из ниже приведенных ответов укажите производительность второго рабочего, если известно, что t — целое число.
производительности второго. Из ниже приведенных ответов укажите производительность второго рабочего, если известно, что t — целое число.
Укажите интервалы, удовлетворяющие неравенству: 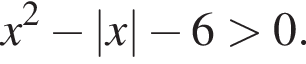

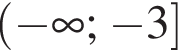


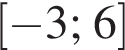
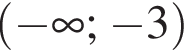
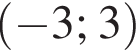
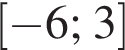
Дана система уравнений
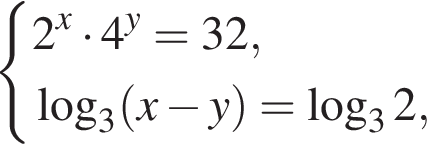
где (x; y) — решение данной системы. Сумма (x + y) принадлежит промежутку?
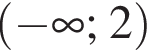
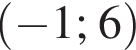
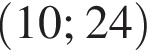
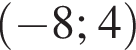
Найдите производную функции: 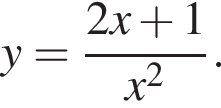
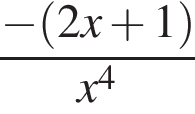
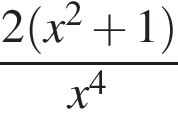
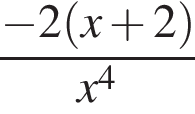
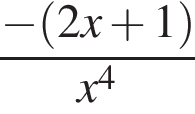
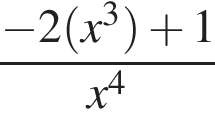
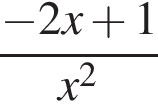
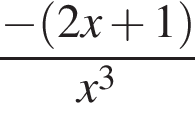
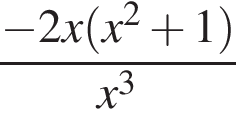
Найдите стороны треугольника MKP, если  и
и  а высота MH = 4 см.
а высота MH = 4 см.
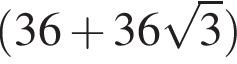 см
см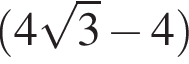 см
смНапишите уравнение общей касательной к параболам: 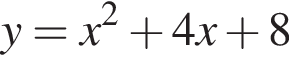 и
и 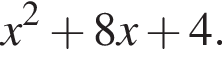
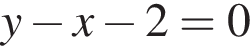

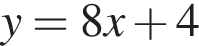
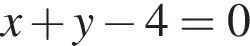
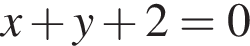
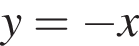
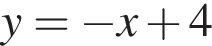

В прямой правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 имеем  и
и  Найдите площадь боковой поверхности и площадь полной поверхности данной призмы.
Найдите площадь боковой поверхности и площадь полной поверхности данной призмы.







