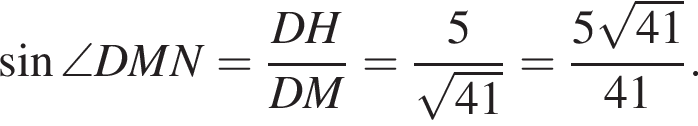1. Тип 1 № 3457 

Источник: ЕНТ по математике 2021 года, вариант 8. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.4\. Вычисление степей и корней
Числовые алгебраические выражения. Задания для подготовки
i
Упростите выражение: 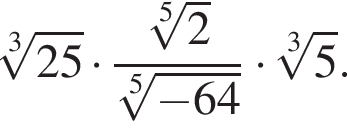
1) −3
2) 2,5
3) −2,5
4) −3,5
Решение. Вычислим:
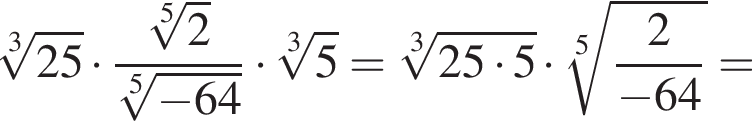
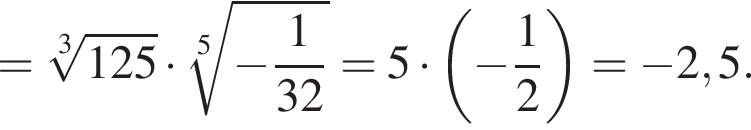
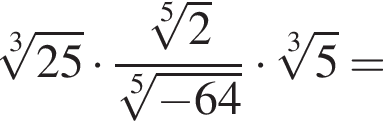
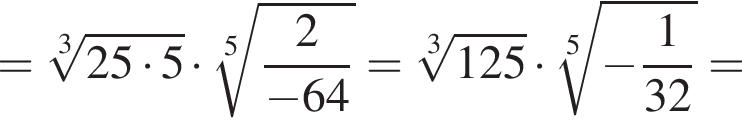
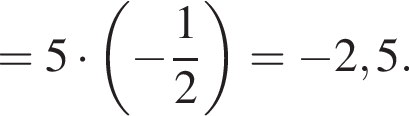
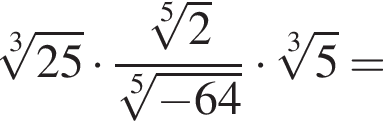
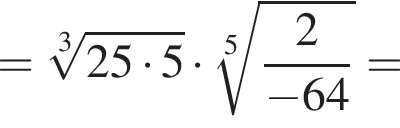
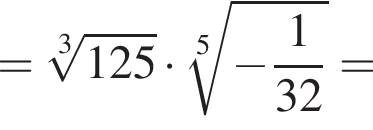
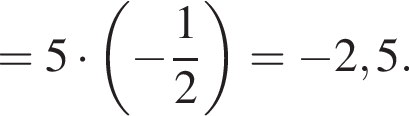
Правильный ответ указан под номером 3.
Ответ: 3
3457
3
Источник: ЕНТ по математике 2021 года, вариант 8. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.4\. Вычисление степей и корней
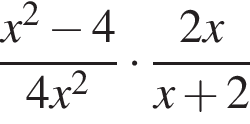 и найдите его значение при
и найдите его значение при 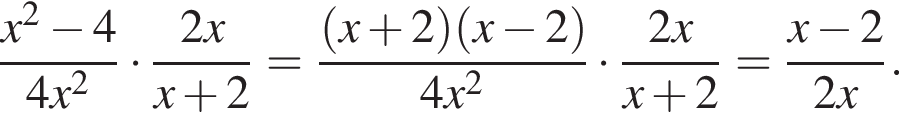
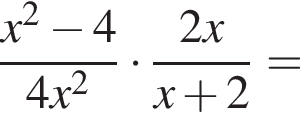
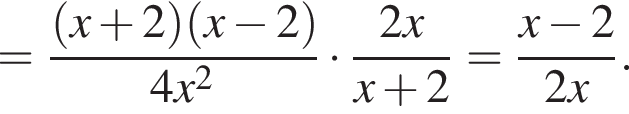
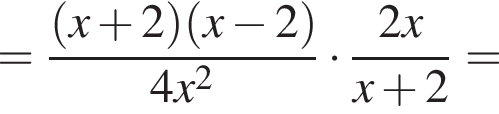
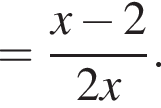
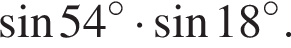
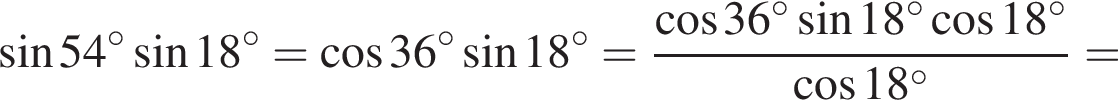
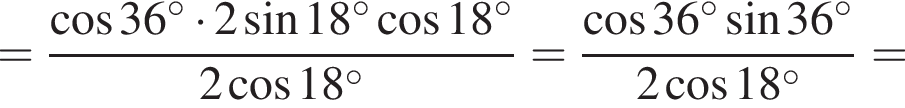
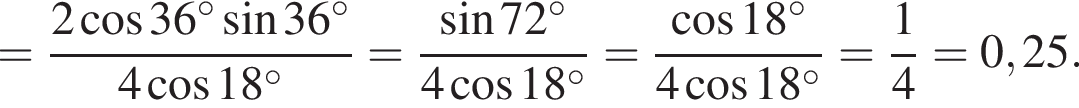
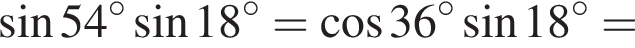
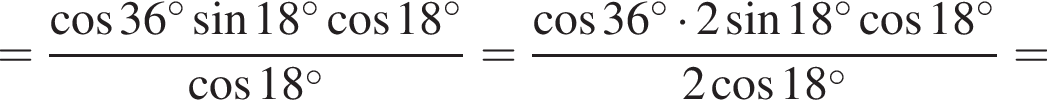
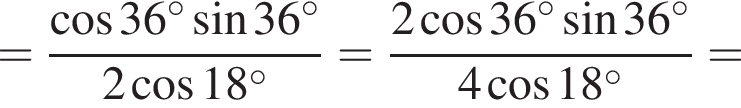
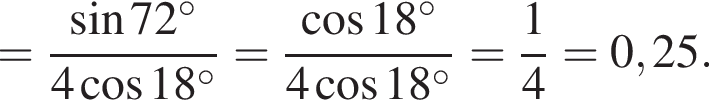
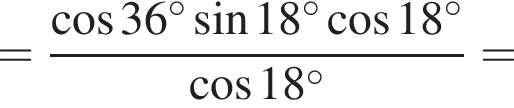
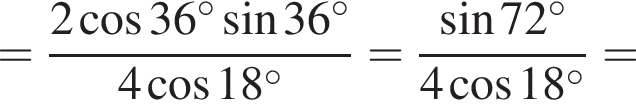
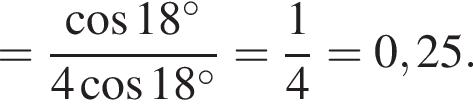
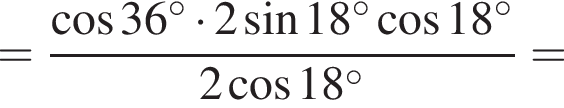
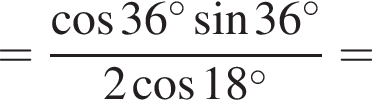


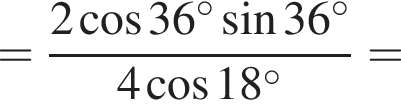
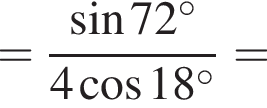
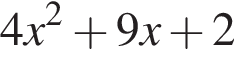 на множители.
на множители.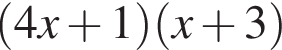
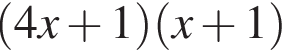
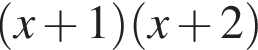
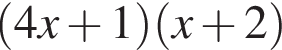
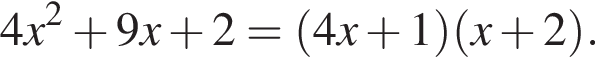

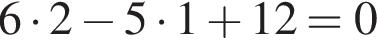 —
—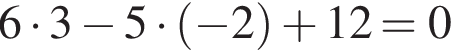 —
—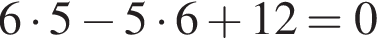 —
—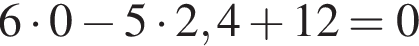 —
—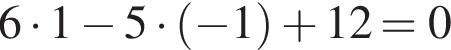 —
—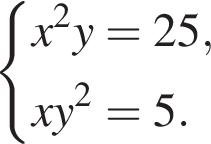
 откуда xy = 5. Вычтем из первого уравнения системы второе, получим
откуда xy = 5. Вычтем из первого уравнения системы второе, получим  откуда x − y = 4.
откуда x − y = 4.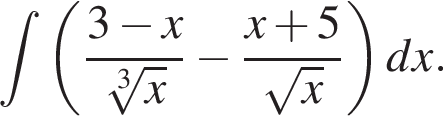
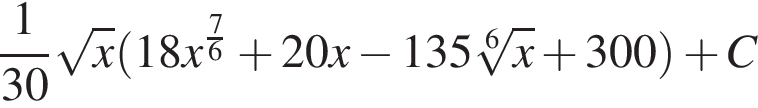
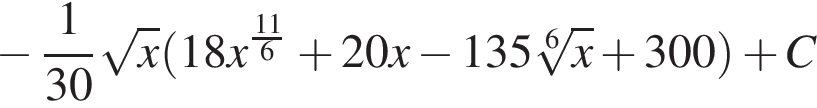
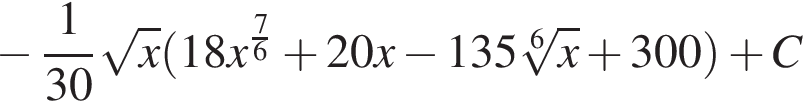
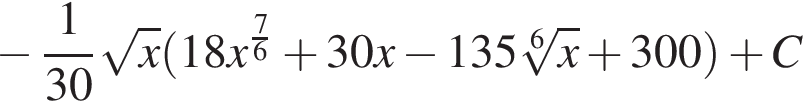
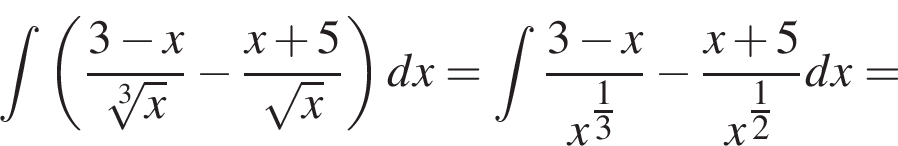
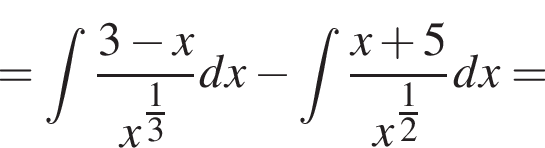

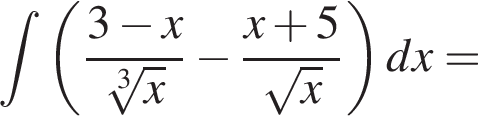
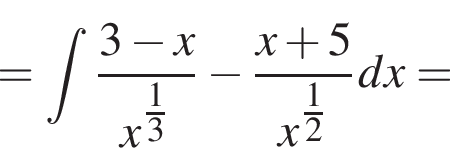
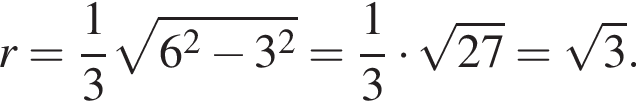
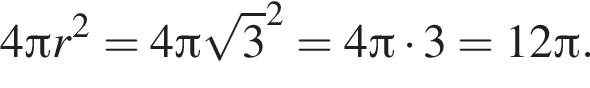
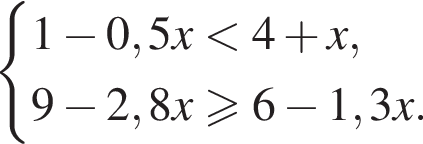
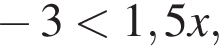 то есть
то есть 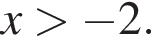 Преобразуя второе неравенство, получим
Преобразуя второе неравенство, получим 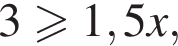 откуда
откуда 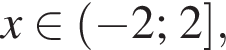 а целыми положительными решениями
а целыми положительными решениями 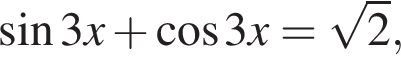 который принадлежит числовому интервалу (90°; 180°).
который принадлежит числовому интервалу (90°; 180°).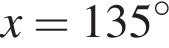 получаем
получаем 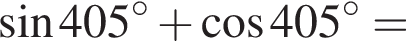

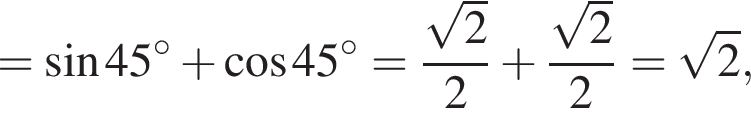

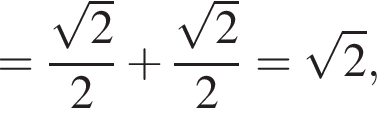
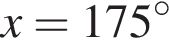 получаем
получаем 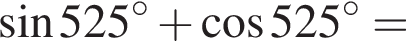

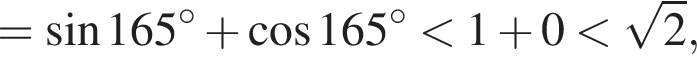
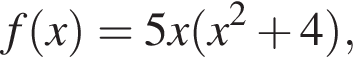 проходящую через точку
проходящую через точку 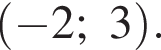
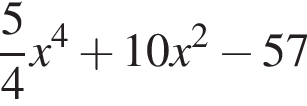
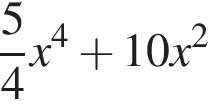
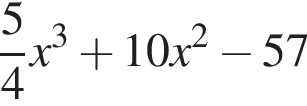
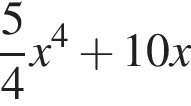

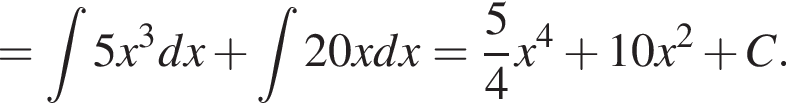
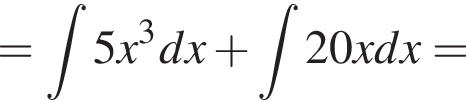
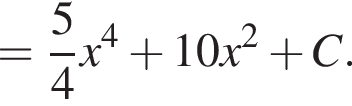
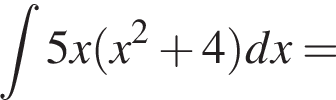
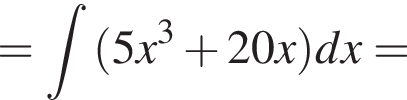
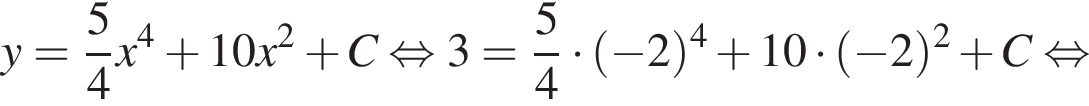

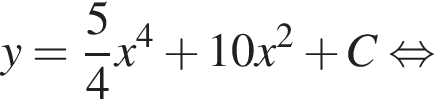
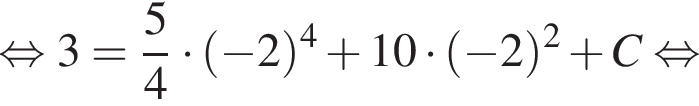


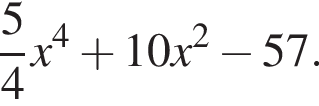
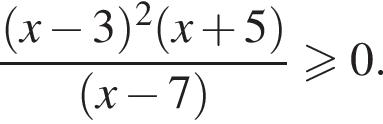
 выражение в левой части равно нулю. При остальных приведенных значениях x числитель положителен, а знаменатель отрицателен, поэтому они не подходят.
выражение в левой части равно нулю. При остальных приведенных значениях x числитель положителен, а знаменатель отрицателен, поэтому они не подходят.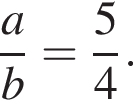 Составим систему уравнений:
Составим систему уравнений: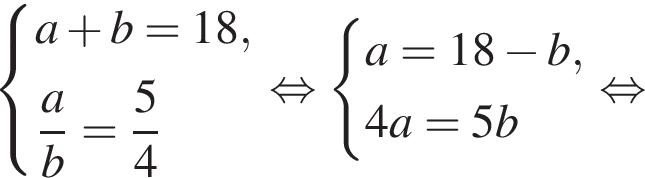
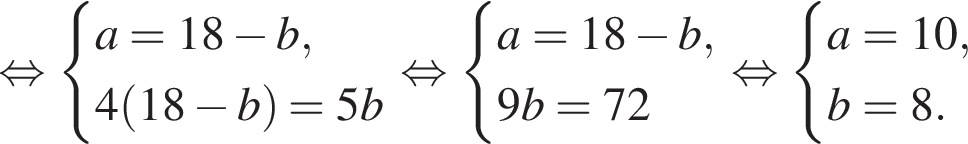
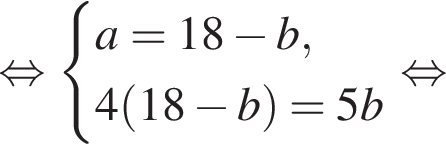
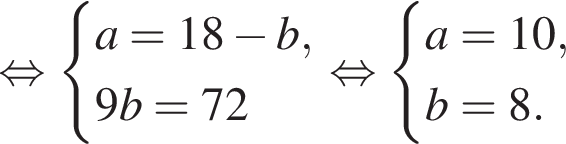
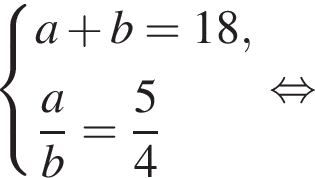
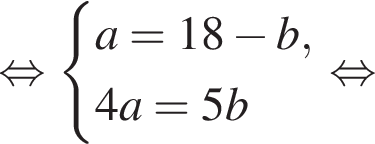
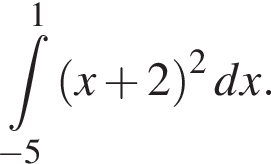
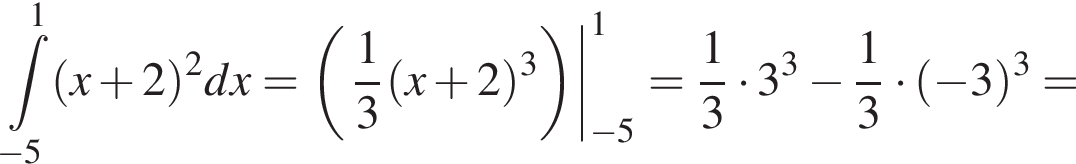
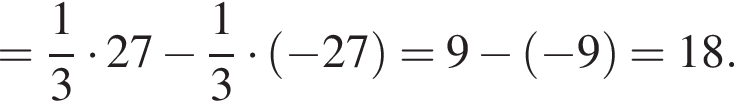
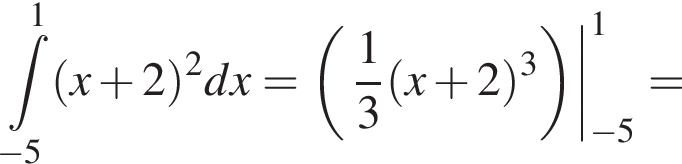
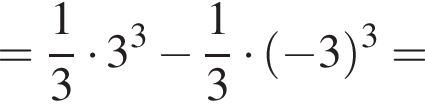
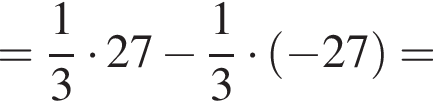
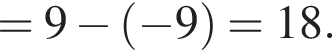
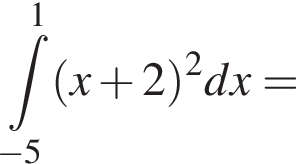

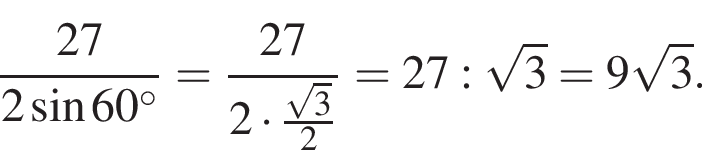
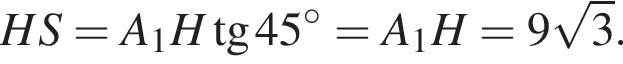
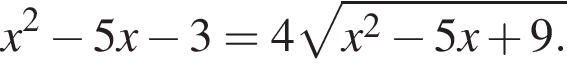
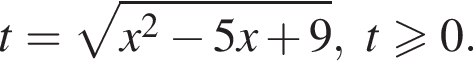 Имеем:
Имеем: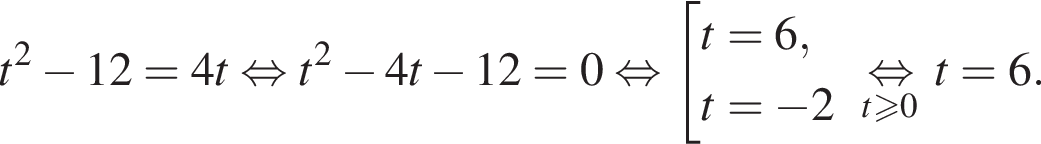
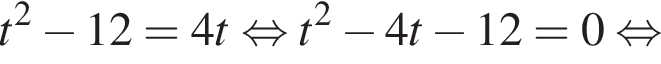
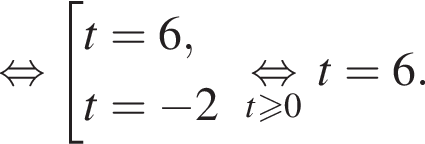

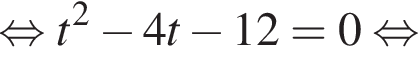
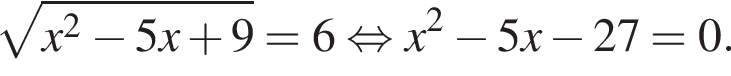 Полученное уравнение имеет один положительный и один отрицательный корень. Согласно теореме Виета, произведение корней уравнения равно −27.
Полученное уравнение имеет один положительный и один отрицательный корень. Согласно теореме Виета, произведение корней уравнения равно −27.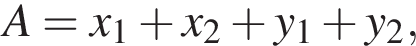 где {
где {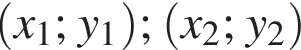 } являются решением системы уравнений:
} являются решением системы уравнений: 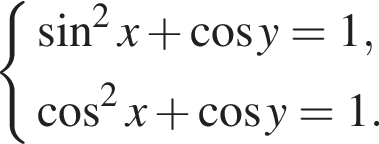
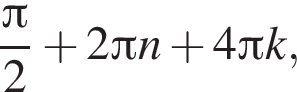
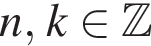

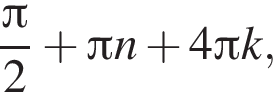

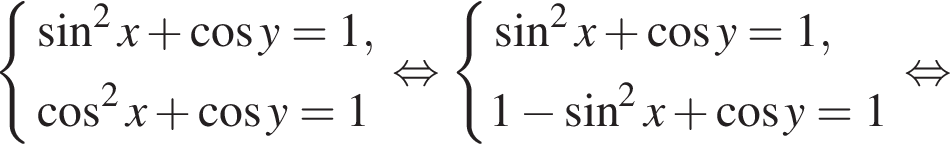
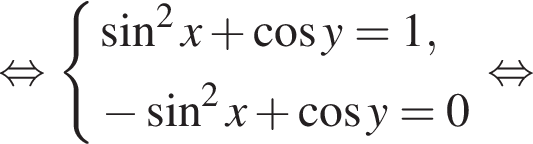
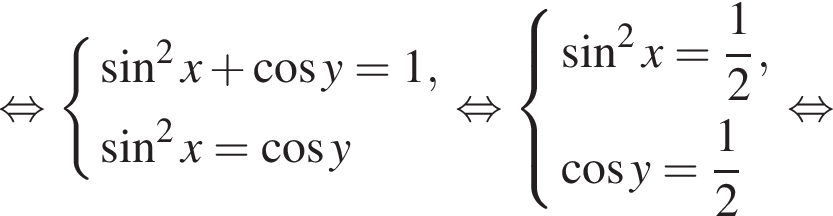
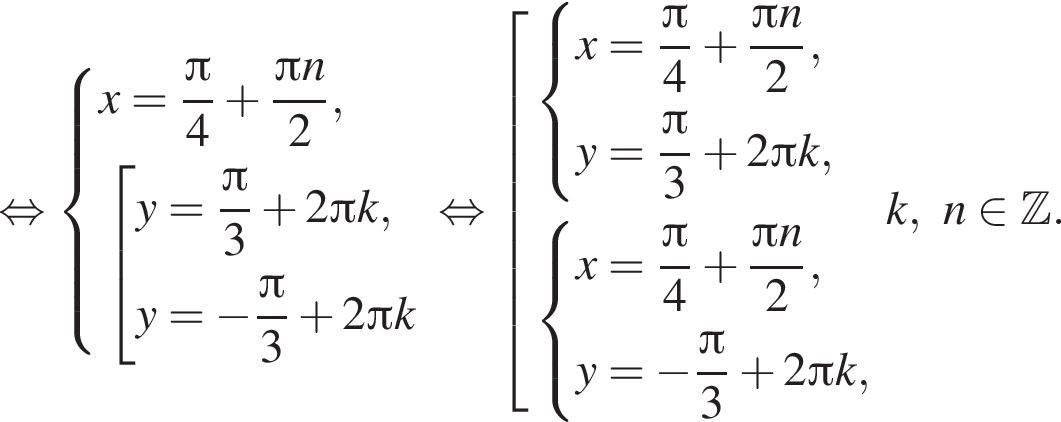
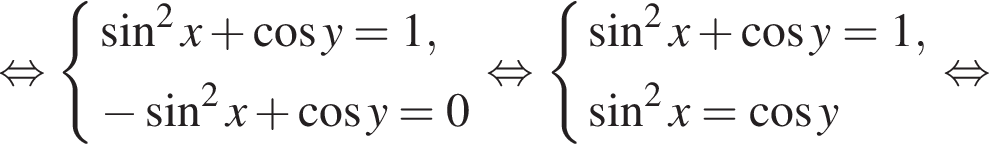
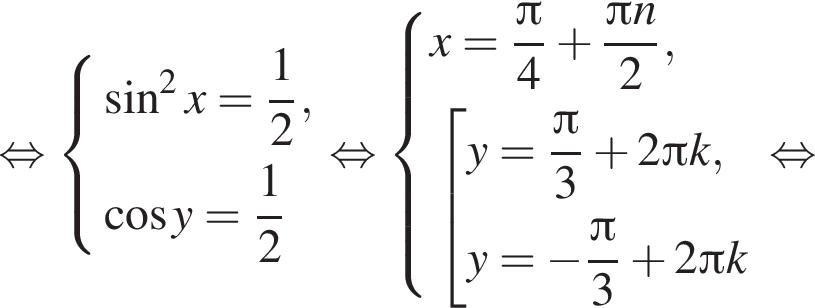
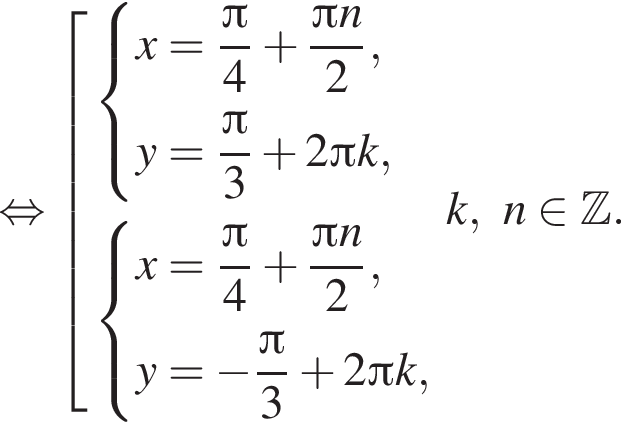
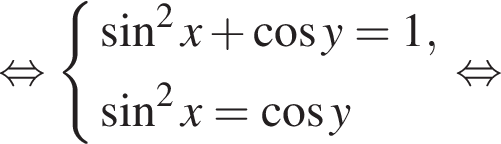
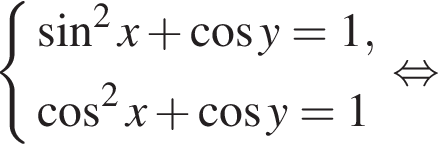
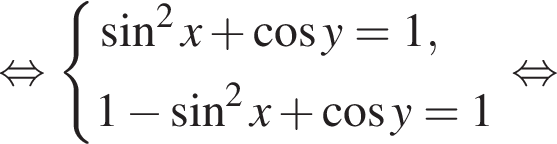
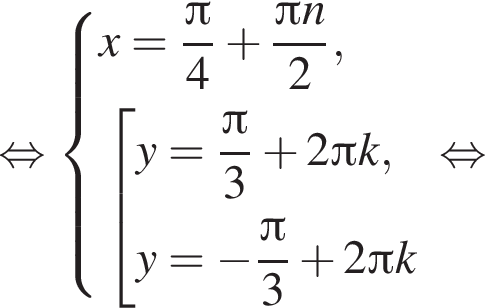
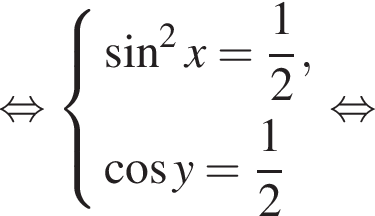

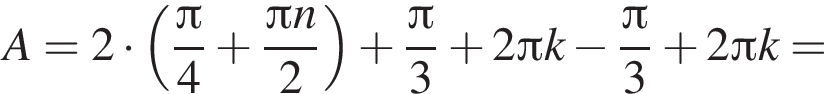
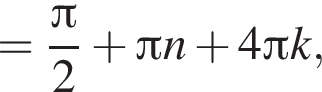
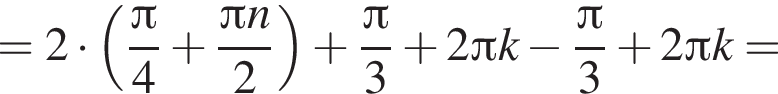

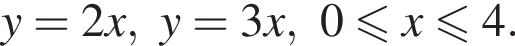
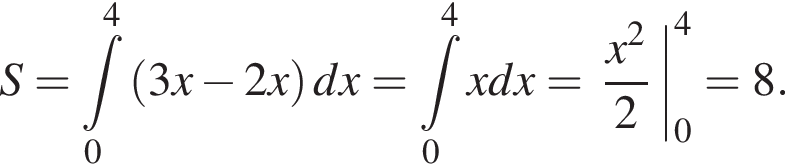
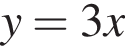 лежит не ниже графика функции
лежит не ниже графика функции 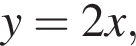 поэтому искомая площадь равна 8.
поэтому искомая площадь равна 8.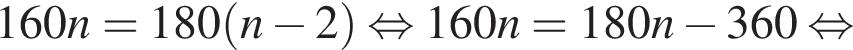

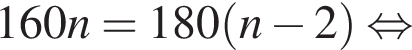
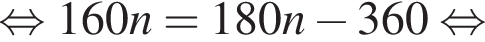
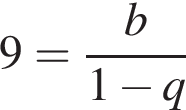 и
и 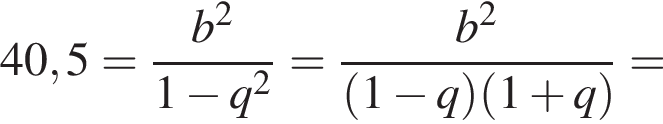

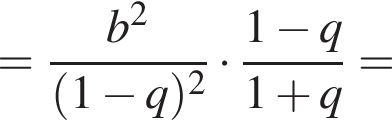
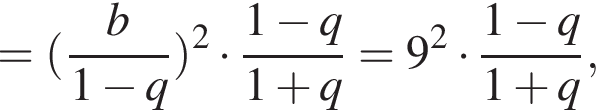
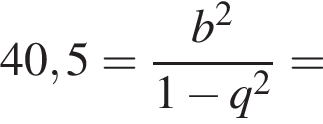
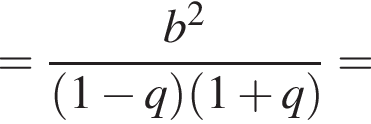
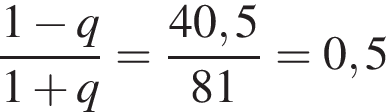

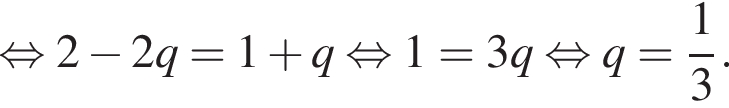

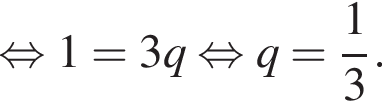
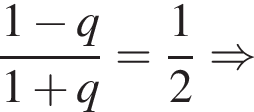
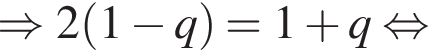
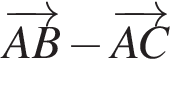 и
и 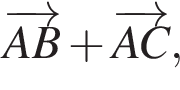 если стороны треугольника равны
если стороны треугольника равны 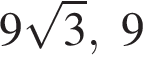
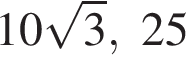
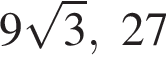
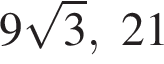
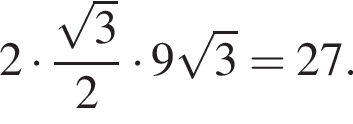
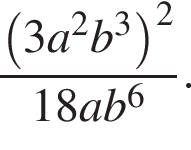

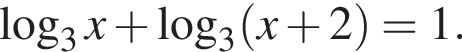
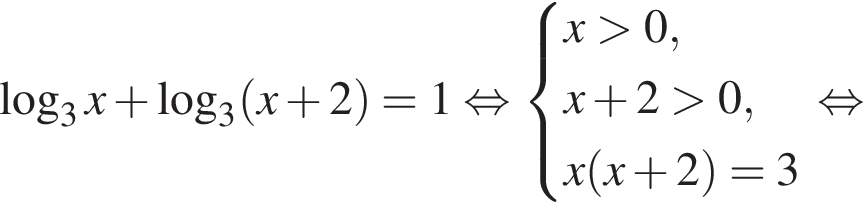
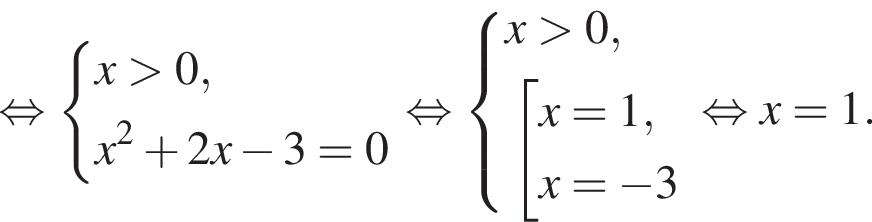
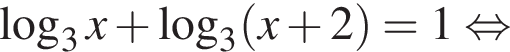
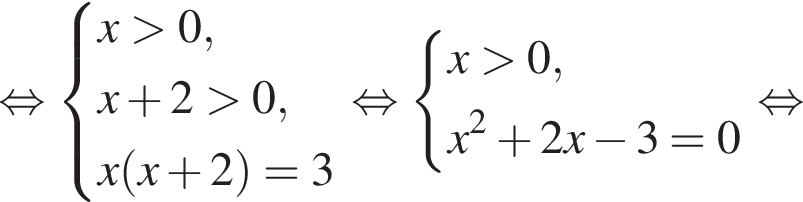

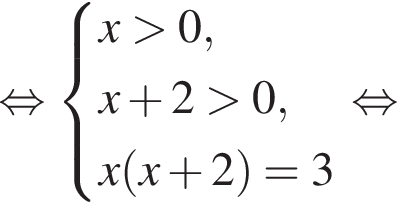
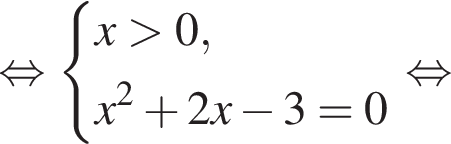
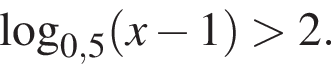
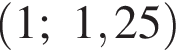
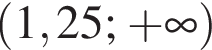

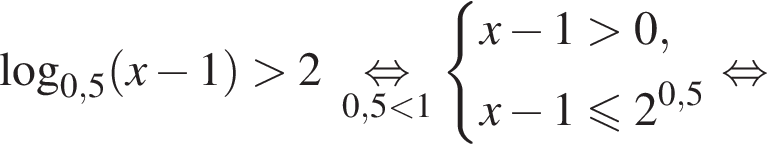
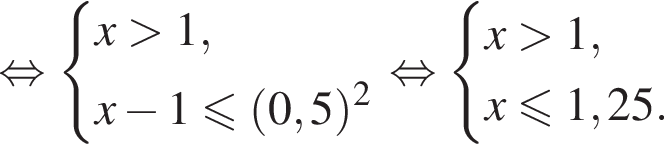
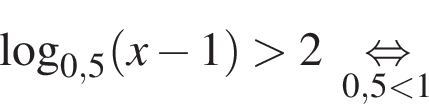
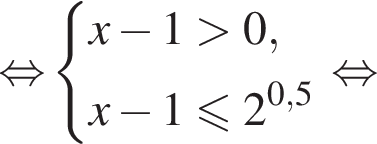
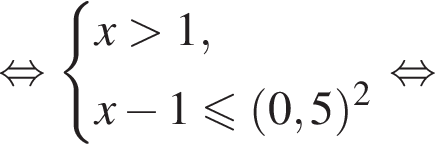
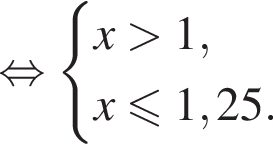
 в точке с абсциссой
в точке с абсциссой 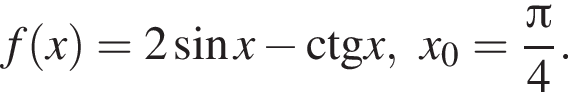
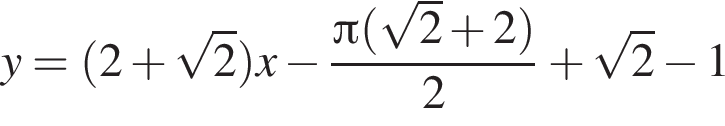
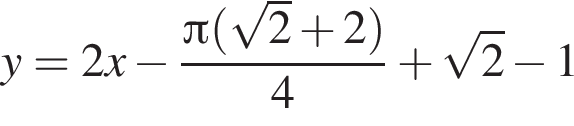
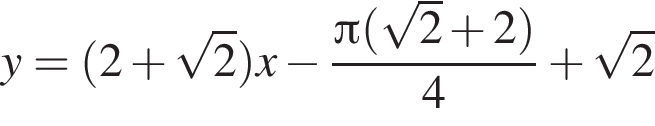
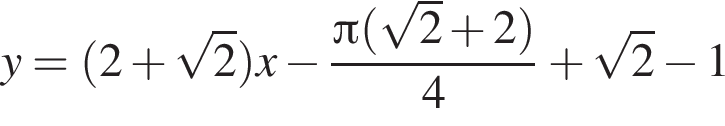
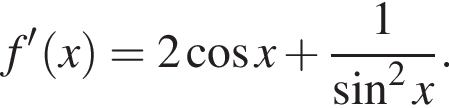 Составим уравнение касательной в точке с абсциссой
Составим уравнение касательной в точке с абсциссой 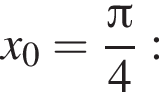
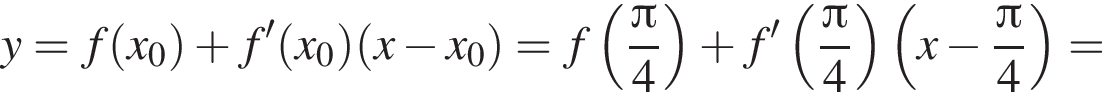
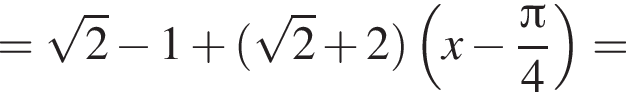
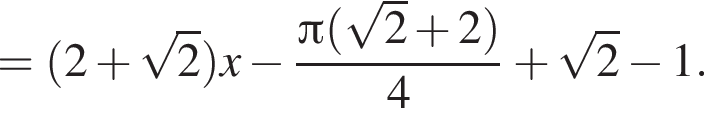
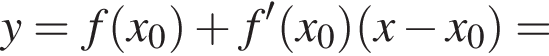
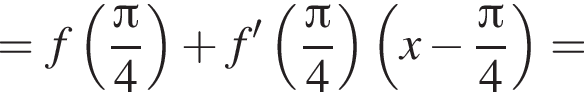




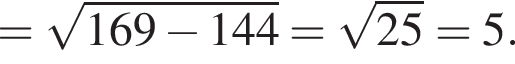
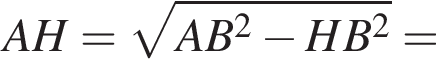
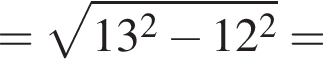
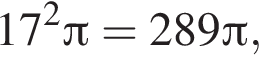 по формуле объема усеченного конуса объем равен
по формуле объема усеченного конуса объем равен 
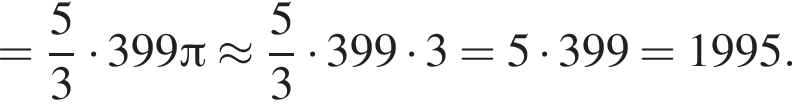
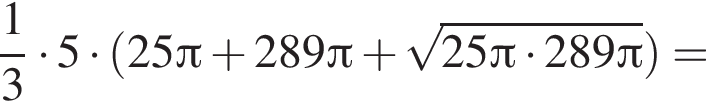
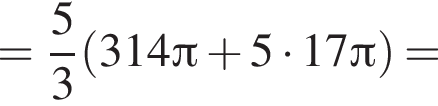
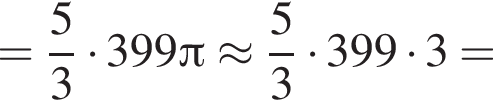

 откуда
откуда 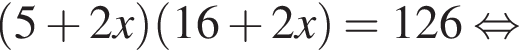
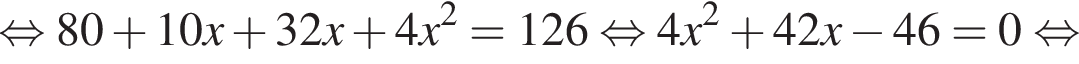

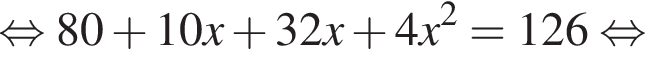

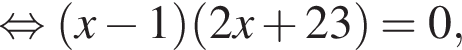

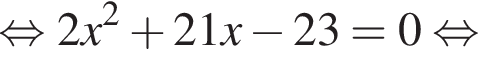
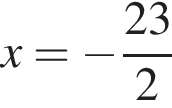 (второе невозможно).
(второе невозможно).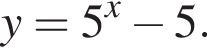 Установите соответствия:
Установите соответствия:

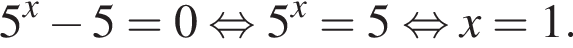
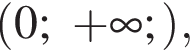 следовательно, множество значений функции
следовательно, множество значений функции 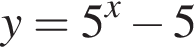 представляет собой промежуток
представляет собой промежуток 
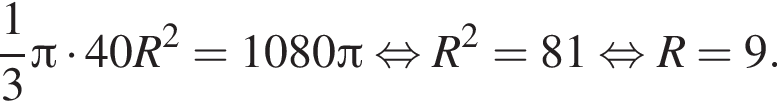
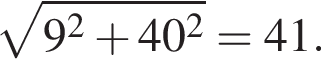 Осевое сечение конуса представляет собой треугольник со сторонами 41, 41, 2 · 9 = 18, а вписанный шар плоскость пересекает по вписанному кругу этого треугольника, причем для шара это тоже сечение, проходящее через центр (он лежит на оси конуса). Значит, осталось найти радиус вписанной окружности треугольника с данными сторонами.
Осевое сечение конуса представляет собой треугольник со сторонами 41, 41, 2 · 9 = 18, а вписанный шар плоскость пересекает по вписанному кругу этого треугольника, причем для шара это тоже сечение, проходящее через центр (он лежит на оси конуса). Значит, осталось найти радиус вписанной окружности треугольника с данными сторонами.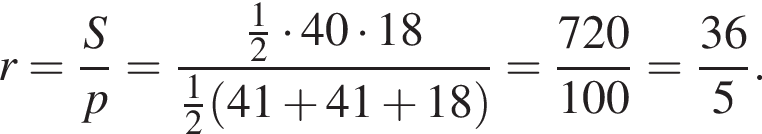
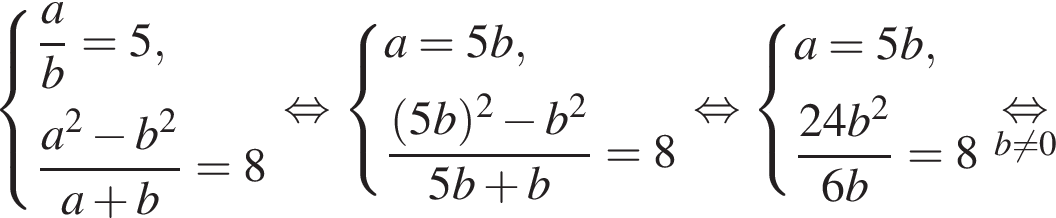
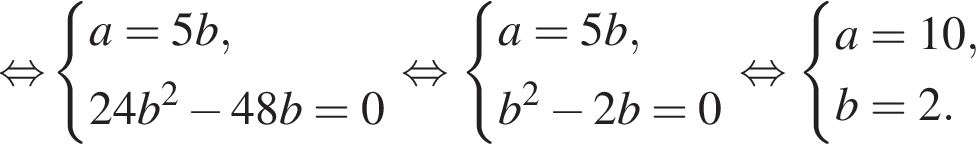
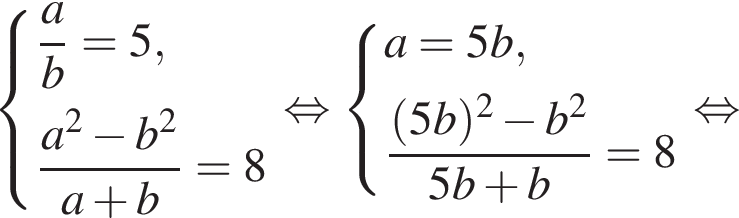
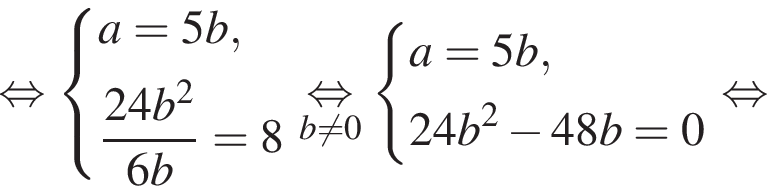
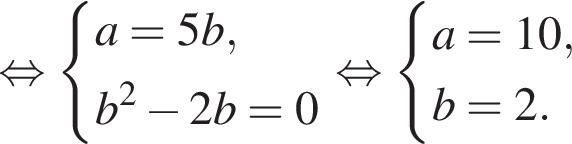
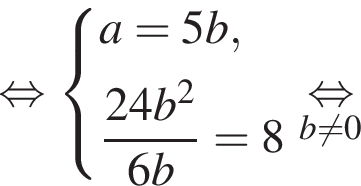
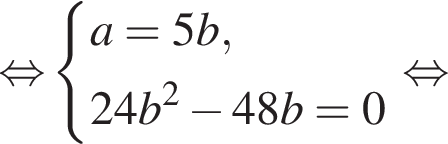
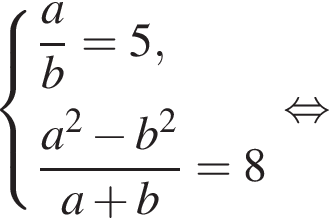
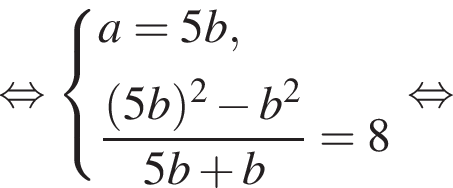
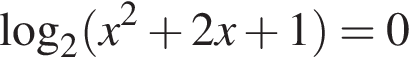 и
и 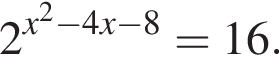 Установите соответствия:
Установите соответствия: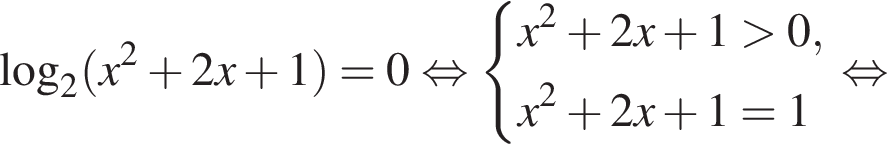
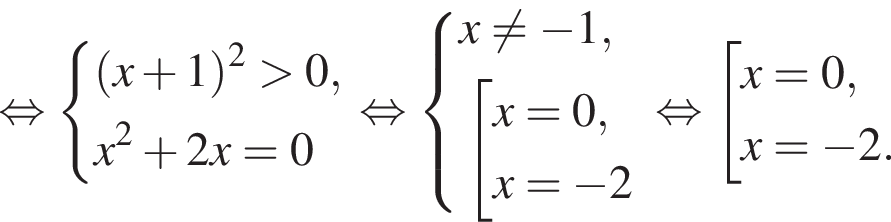
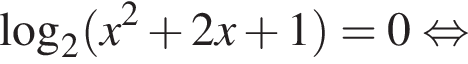
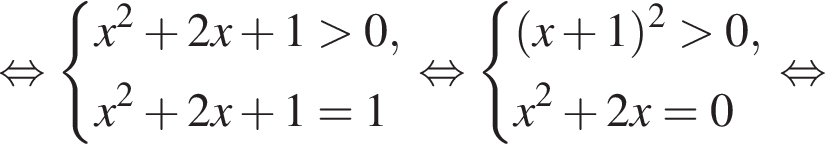
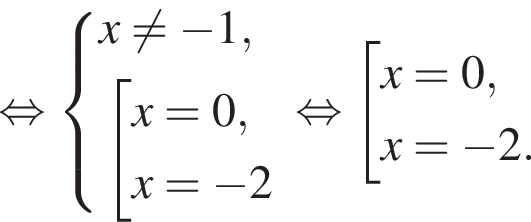
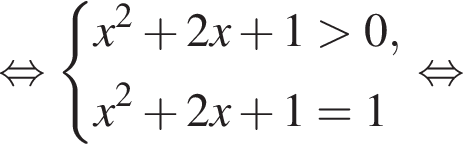
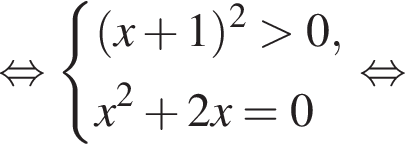
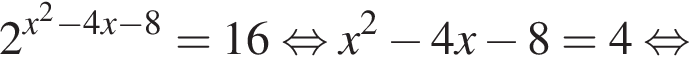
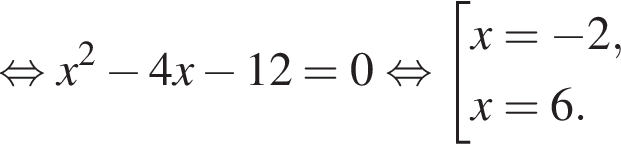
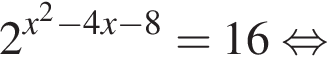
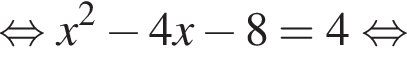
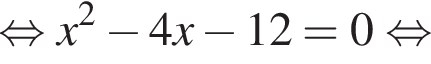
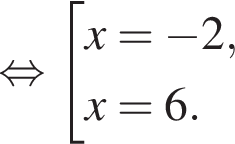
 Установите соответствие между выражением и его числовым значением.
Установите соответствие между выражением и его числовым значением.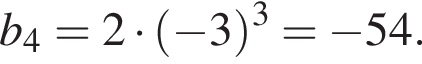 Найдем сумму первых трех членов прогрессии:
Найдем сумму первых трех членов прогрессии: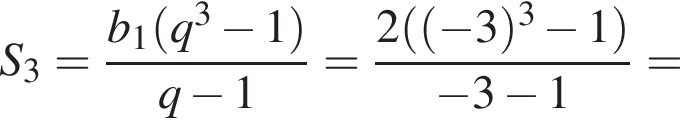
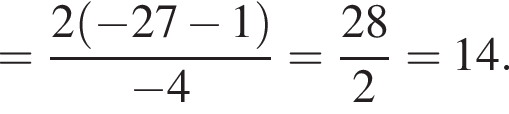
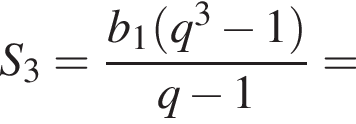
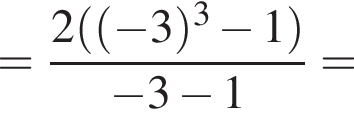
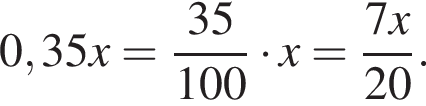
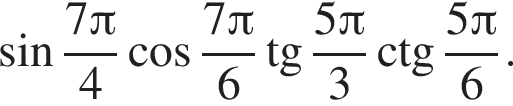
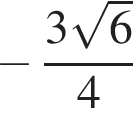
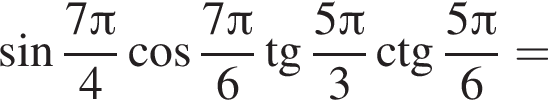
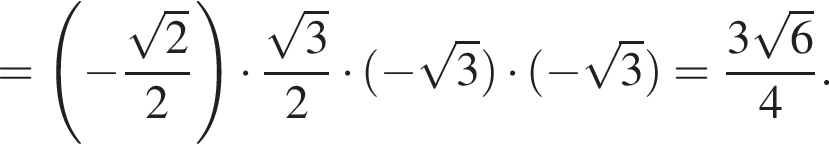
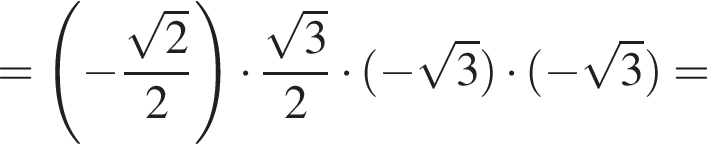
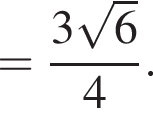
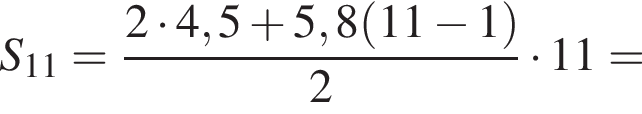
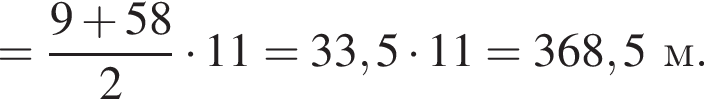
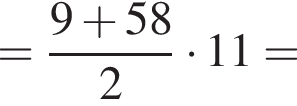
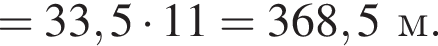
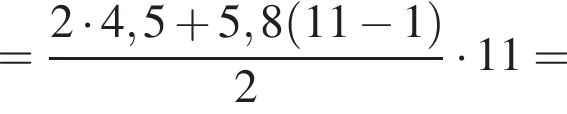
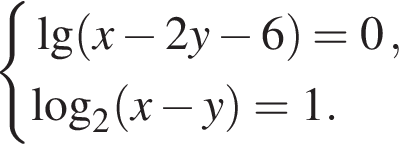
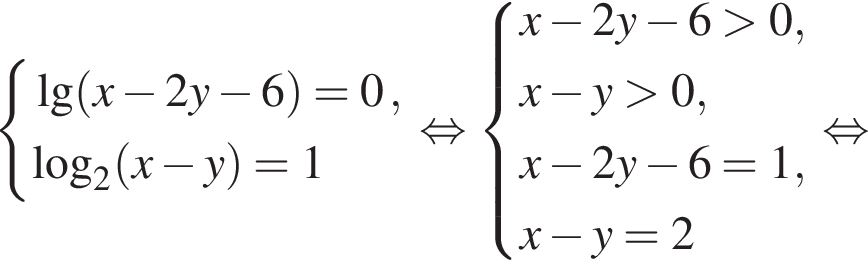
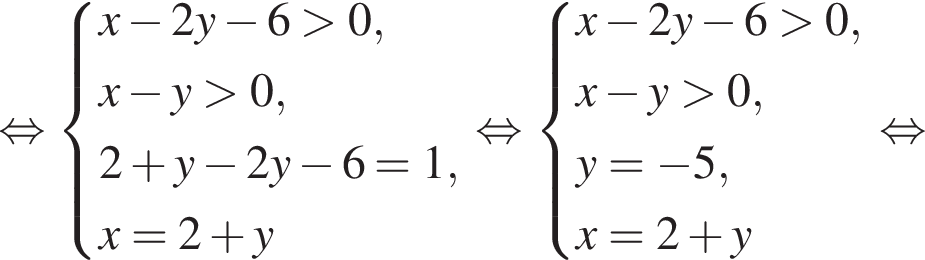

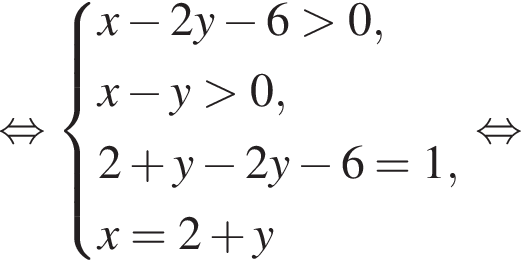

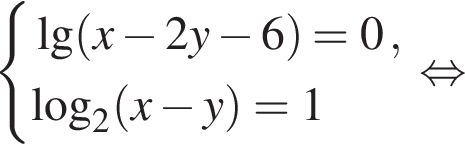
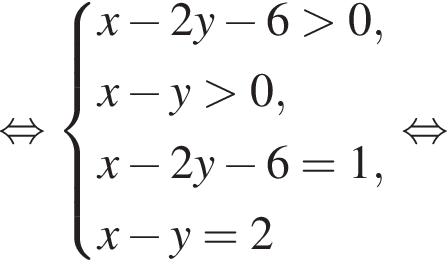
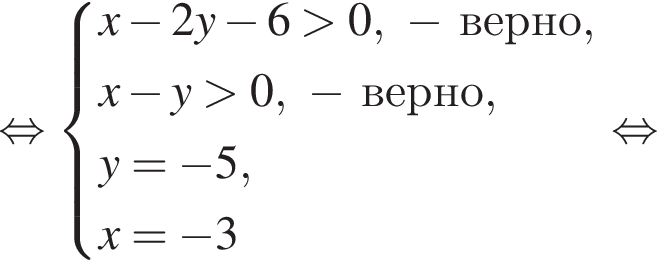
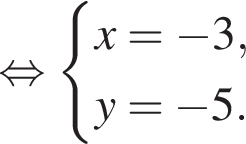
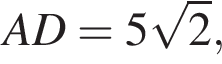 AB = 3.
AB = 3.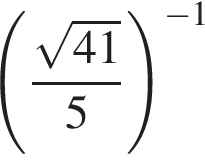
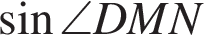 — искомый.
— искомый.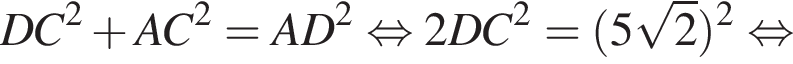
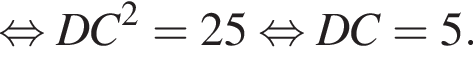
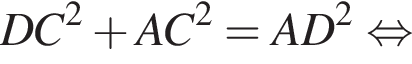
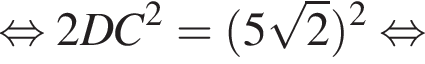

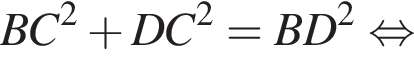
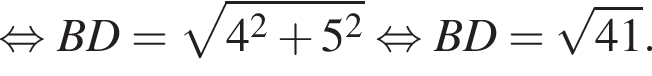


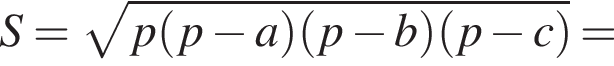
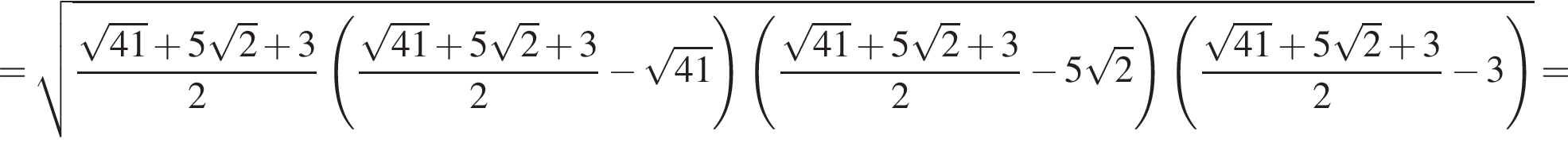
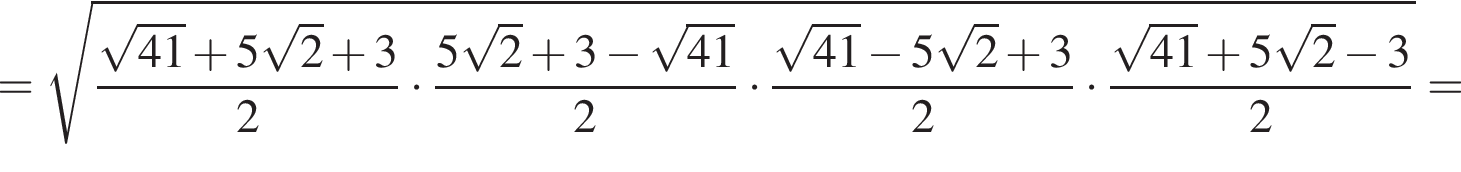
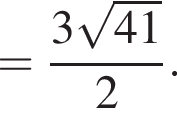
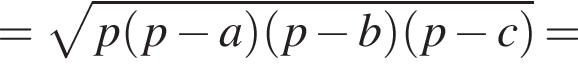
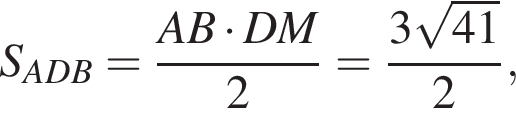
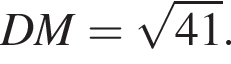 В треугольнике DMN проведем высоту DH к стороне MN, DH = DC = 5. Имеем:
В треугольнике DMN проведем высоту DH к стороне MN, DH = DC = 5. Имеем: