Верным разложением числа 660 на простые множители является:
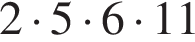
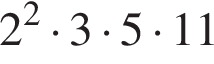
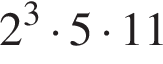
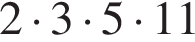
Верным разложением числа 660 на простые множители является:
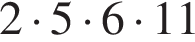
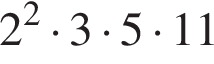
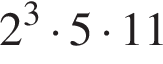
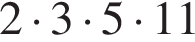
Выполните действие 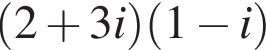 и определите действительную часть числа
и определите действительную часть числа
3начение выражения 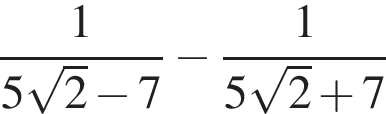 кратно?
кратно?
Найдите значение выражения 
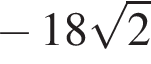
Hекоторое двузначное число разделили на разность его цифр. Какое выражение удовлетворяет данному условию?
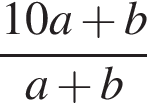
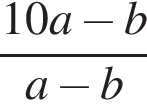
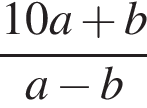
Pешите неравенство: 
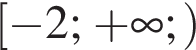
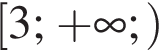
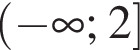
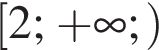
Решите систему уравнений: 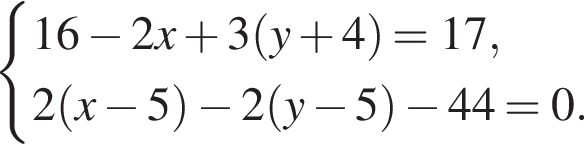
Найдите предел в точке 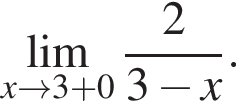
Внутренний угол правильного многоугольника равен 172°. Количество сторон данного многоугольника равно
Найдите объём куба, если площадь его полной поверхности равна 72 см2.
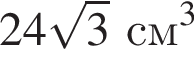
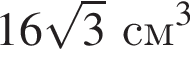
Решите уравнение: 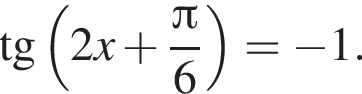
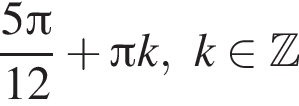
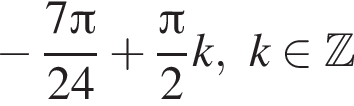
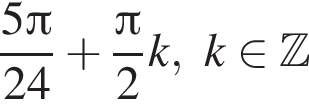
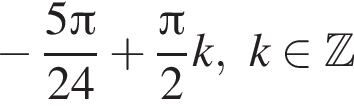
Решите систему неравенств: 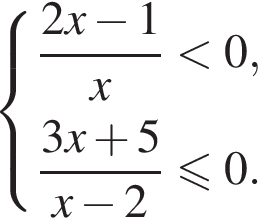

Вычислите 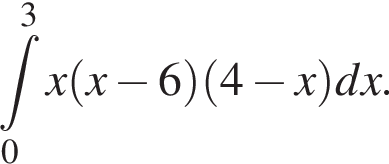
Сколькими способами можно переставлять буквы в слове перешеек так, чтобы четыре буквы е не шли подряд?
К окружности проведена секущая CA. Треугольник BOE равносторонний, CA = 12. Длина касательной CE равна
Даны векторы: 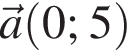 и
и 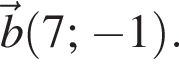 Косинус угла между векторами
Косинус угла между векторами  и
и 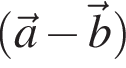 равен?
равен?

Пусть x0 — наибольший корень уравнения 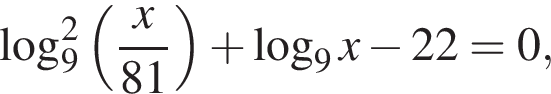 тогда значение выражения
тогда значение выражения ![]() равно ...
равно ...
Решите систему уравнений: 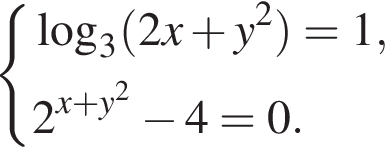
Найдите первообразную функции 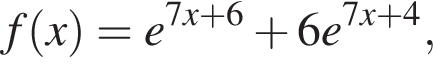 проходящую через точку
проходящую через точку ![]()
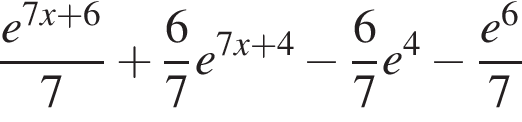
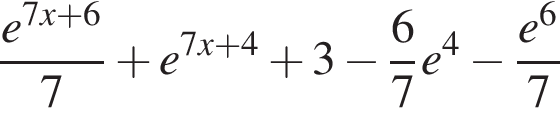
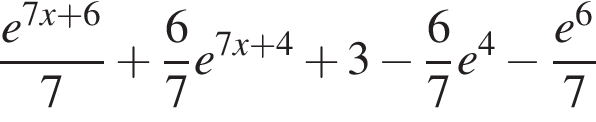
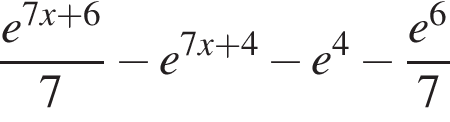
Цилиндр с радиусом основания  вписан в правильную треугольную призму. Найдите площадь одной боковой грани призмы, если высота цилиндра 7 см.
вписан в правильную треугольную призму. Найдите площадь одной боковой грани призмы, если высота цилиндра 7 см.
Чайный двор
Посуда является товаром народного потребления и оценивается не только как предмет быта, но и как элемент декора. Спрос на нее всегда остается на достаточно высоком уровне по ряду причин. На сегодняшний день рынок представлен многообразием товаров различных видов посуды и ценовых категорий, что позволяет удовлетворить любой спрос.
В магазине «Чайный двор» выставлены на продажу различный ассортимент чайной посуды начиная от ложки для чая, заканчивая посудой для чайных церемоний из различных металлов и материалов. По акции продавались 5 чашек, 8 блюдцев, 7 ложек. Мадина купила домой комплект посуды по акции.
Сколькими способами Мадина может выбрать в магазине комплект «чашка+блюдце+ложка»?
Чайный двор
Посуда является товаром народного потребления и оценивается не только как предмет быта, но и как элемент декора. Спрос на нее всегда остается на достаточно высоком уровне по ряду причин. На сегодняшний день рынок представлен многообразием товаров различных видов посуды и ценовых категорий, что позволяет удовлетворить любой спрос.
В магазине «Чайный двор» выставлены на продажу различный ассортимент чайной посуды начиная от ложки для чая, заканчивая посудой для чайных церемоний из различных металлов и материалов. По акции продавались 5 чашек, 8 блюдцев, 7 ложек. Мадина купила домой комплект посуды по акции.
Сколькими способами Мадина может выбрать в магазине комплект «чашка+блюдце»?
Чайный двор
Посуда является товаром народного потребления и оценивается не только как предмет быта, но и как элемент декора. Спрос на нее всегда остается на достаточно высоком уровне по ряду причин. На сегодняшний день рынок представлен многообразием товаров различных видов посуды и ценовых категорий, что позволяет удовлетворить любой спрос.
В магазине «Чайный двор» выставлены на продажу различный ассортимент чайной посуды начиная от ложки для чая, заканчивая посудой для чайных церемоний из различных металлов и материалов. По акции продавались 5 чашек, 8 блюдцев, 7 ложек. Мадина купила домой комплект посуды по акции.
Сколькими способами Мадина может выбрать в магазине из данных товаров комплект из двух разных предметов?
Чайный двор
Посуда является товаром народного потребления и оценивается не только как предмет быта, но и как элемент декора. Спрос на нее всегда остается на достаточно высоком уровне по ряду причин. На сегодняшний день рынок представлен многообразием товаров различных видов посуды и ценовых категорий, что позволяет удовлетворить любой спрос.
В магазине «Чайный двор» выставлены на продажу различный ассортимент чайной посуды начиная от ложки для чая, заканчивая посудой для чайных церемоний из различных металлов и материалов. По акции продавались 5 чашек, 8 блюдцев, 7 ложек. Мадина купила домой комплект посуды по акции.
Сколькими способами Мадина может купить в магазине комплект «2 чашки+блююце+3 ложки»?
Чайный двор
Посуда является товаром народного потребления и оценивается не только как предмет быта, но и как элемент декора. Спрос на нее всегда остается на достаточно высоком уровне по ряду причин. На сегодняшний день рынок представлен многообразием товаров различных видов посуды и ценовых категорий, что позволяет удовлетворить любой спрос.
В магазине «Чайный двор» выставлены на продажу различный ассортимент чайной посуды начиная от ложки для чая, заканчивая посудой для чайных церемоний из различных металлов и материалов. По акции продавались 5 чашек, 8 блюдцев, 7 ложек. Мадина купила домой комплект посуды по акции.
Мадина купила комплект из 5 чашек: 3 из них серебряные, 2 простые; 8 блюдцев: 5 серебряных, 3 простых; 7 ложек: 5 серебряных, 2 простых. Сколькими способами Мадина может выбрать комплект предметов, состоящих из двух серебряных чашек, трех серебряных блюдцев и одной простой ложки.
Из нижеперечисленных ответов укажите те, 35% которых являются целым числом.
Решите уравнение, приводимое к квадратному, относительно тригонометрической функции 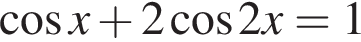 .
.
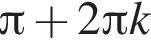
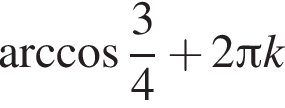
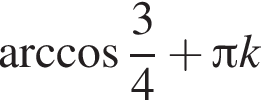
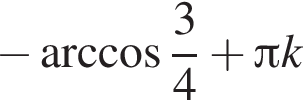
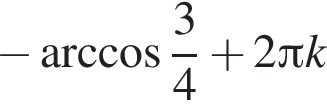
Вынесите множители из-под знака корня в выражении 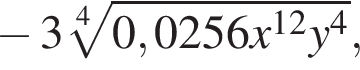 при
при ![]() и
и ![]()
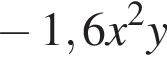
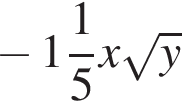
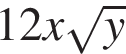
Укажите промежутки, в которых лежат экстремумы функции: 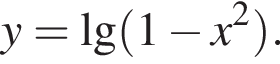
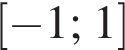
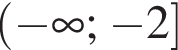
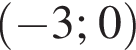

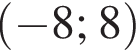
Упростите выражение: 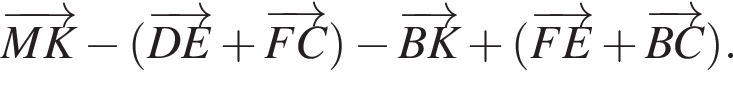
Вычислите 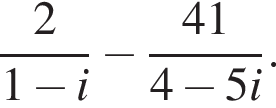
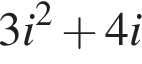
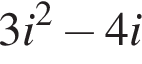


Решением неравенства 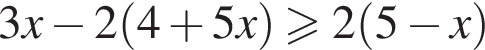 является промежуток?
является промежуток?
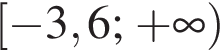
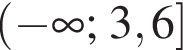
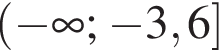

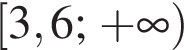
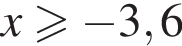
В треугольнике ABC известно, что  см,
см,  см и
см и  см. Найдите все верные утверждения.
см. Найдите все верные утверждения.
Последовательность (bn) геометрическая прогрессия. Найдите: b4, если 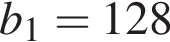 и
и 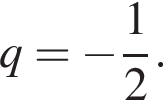
Прямая OO1 — ось цилиндра. Найдите площадь боковой поверхности цилиндра, если площадь CC1E1E равна Q.