Дана SABCD пирамида, SO — высота, АВСD — прямоугольник. Вычислите площадь полной поверхности пирамиды, если AD = 6, DC = 8 и SO = 4.
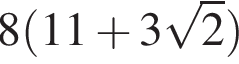
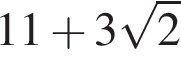
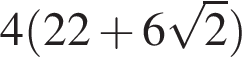
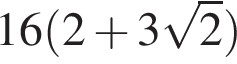
Решение. Знаем, что
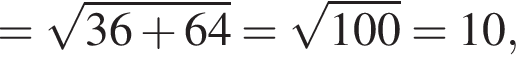
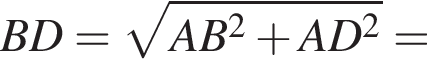
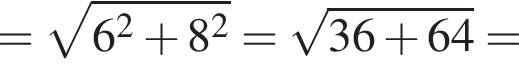
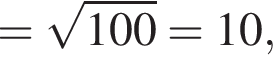
а поскольку диагонали прямоугольника равны и пересекаются в середине,
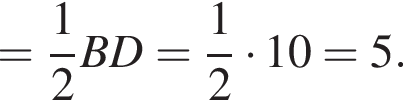
Все прямоугольные треугольники AOS, BOS, COS, DOS равны по двум катетам, поэтому и все их гипотенузы равны
Среди боковых граней пирамиды два равнобедренных треугольника с боковой стороной 
и основанием 8, с высотами равными
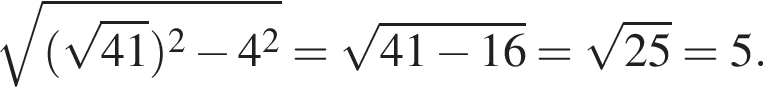
И два равнобедренных треугольника с боковой стороной и основанием 6, с высотами равными
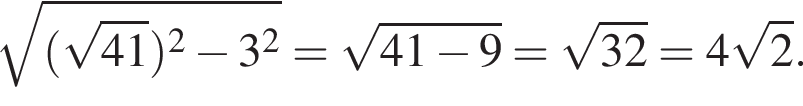
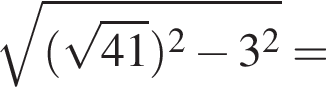
Значит, площадь полной поверхности равна
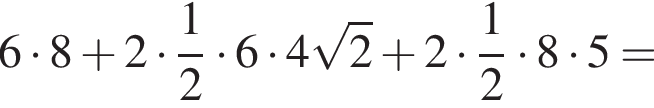
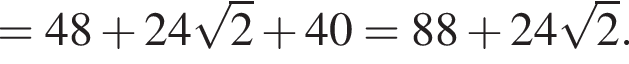
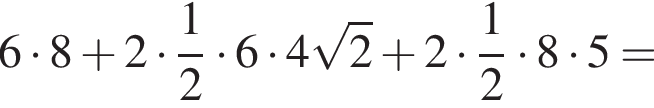
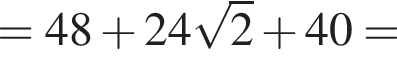
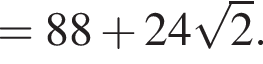
Этому выражению равны ответы 1 и 4, просто по-разному записаны.
Правильные ответы указаны под номерами 1 и 4.