В трапецию, у которой нижнее основание в два раза больше верхнего и боковая сторона равна 9, вписана окружность. Радиус окружности равен:
Решение. У любого описанного четырехугольника суммы противоположных сторон равны. Пусть верхнее основание трапеции имеет длину x, а нижнее 2x, тогда
Опустим из B и C — вершин меньшего основания — перпендикуляры BH и CK на AD (см. рисунок). Тогда
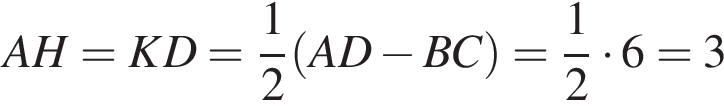
и по теореме Пифагора для треугольника ABH получаем
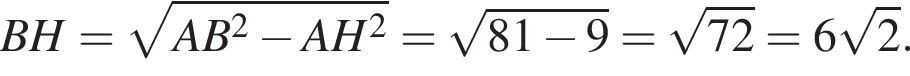
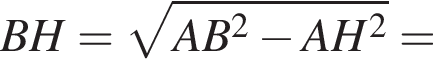
Значит, расстояние между основаниями трапеции равно 
С другой стороны, один из диаметров вписанной окружности тоже представляет собой такое расстояние. Значит, радиус окружности равен 
Правильный ответ указан под номером 4.